Функция Розенброка - Rosenbrock function

График функции Розенброка двух переменных. Здесь

{displaystyle a = 1, b = 100}

, а минимальное значение нуля - при

{displaystyle (1,1)}

.

В математическая оптимизация, то Функция Розенброка не-выпуклая функция, представлен Говард Х. Розенброк в 1960 году, который используется как проблема теста производительности для оптимизации алгоритмы.^[1] Он также известен как Долина Розенброка или же Банановая функция Розенброка.

Глобальный минимум находится внутри длинного узкого параболический в форме плоской долины. Найти долину - тривиально. Сойтись к глобальному минимум Однако это сложно.

Функция определяется как

${displaystyle f (x, y) = (a-x) ^ {2} + b (y-x ^ {2}) ^ {2}}$

Его глобальный минимум составляет ${displaystyle (x, y) = (a, a ^ {2})}$ , куда ${displaystyle f (x, y) = 0}$ . Обычно эти параметры устанавливаются так, что ${displaystyle a = 1}$ и ${displaystyle b = 100}$ . Только в тривиальном случае, когда ${displaystyle a = 0}$ функция симметрична, и минимум находится в начале координат.

Многомерные обобщения

Обычно встречаются два варианта.

Анимация функции трех переменных Розенброка. ^[2]

Один - это сумма ${displaystyle N / 2}$ несвязанных двухмерных задач Розенброка и определяется только для четных ${displaystyle N}$ s:

{displaystyle f (mathbf {x}) = f (x_ {1}, x_ {2}, dots, x_ {N}) = sum _ {i = 1} ^ {N / 2} left [100 (x_ {2i -1} ^ {2} -x_ {2i}) ^ {2} + (x_ {2i-1} -1) ^ {2} ight].}

^[3]

У этого варианта есть предсказуемо простые решения.

Второй, более сложный вариант:

{displaystyle f (mathbf {x}) = sum _ {i = 1} ^ {N-1} [100 (x_ {i + 1} -x_ {i} ^ {2}) ^ {2} + (1- x_ {i}) ^ {2}] quad {mbox {where}} quad mathbf {x} = (x_ {1}, ldots, x_ {N}) в mathbb {R} ^ {N}.}

^[4]

имеет ровно один минимум для ${displaystyle N = 3}$ (в ${displaystyle (1,1,1)}$ ) и ровно два минимума для ${displaystyle 4leq Nleq 7}$ - глобальный минимум всех единиц и локальный минимум около ${displaystyle {hat {mathbf {x}}} = (- 1,1, точки, 1)}$ . Этот результат получается путем установки градиента функции равным нулю с учетом того, что полученное уравнение является рациональной функцией ${displaystyle x}$ . Для малых ${displaystyle N}$ полиномы могут быть определены точно и Теорема Штурма можно использовать для определения количества реальных корней, в то время как корни могут быть ограниченный в районе ${displaystyle | x_ {i} | <2,4}$ .^[5] Для большего ${displaystyle N}$ этот метод не работает из-за размера задействованных коэффициентов.

Стационарные точки

Многие из стационарных точек функции при построении демонстрируют регулярный узор.^[5] Эту структуру можно использовать для их обнаружения.

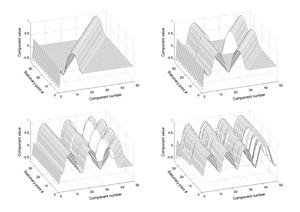
Корни розенброка со структурой горба

Примеры оптимизации

Применение метода Нелдера-Мида к функции Розенброка

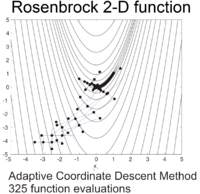
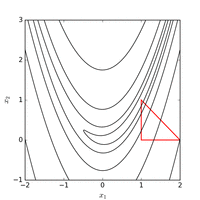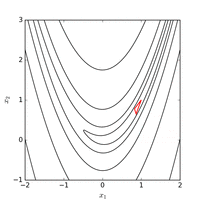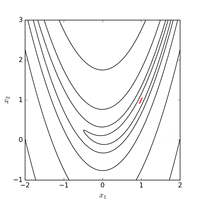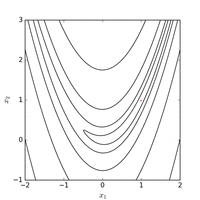
Функцию Розенброка можно эффективно оптимизировать путем адаптации соответствующей системы координат без использования каких-либо информация о градиенте и без построения локальных моделей аппроксимации (в отличие от многих оптимизаторов без производных). На следующем рисунке показан пример двумерной оптимизации функции Розенброка с помощьюадаптивный координатный спуск от отправной точки ${displaystyle x_ {0} = (- 3, -4)}$ . Решение со значением функции ${displaystyle 10 ^ {- 10}}$ можно найти после 325 оценок функций.

С использованием Метод Нелдера – Мида от отправной точки ${displaystyle x_ {0} = (- 1,1)}$ при регулярном начальном симплексе минимум находится со значением функции ${displaystyle 1.36cdot 10 ^ {- 10}}$ после 185 оценок функций. На рисунке ниже показана эволюция алгоритма.

Смотрите также

Тестовые функции для оптимизации

внешняя ссылка

[1] Розенброк, HH (1960). «Автоматический метод определения наибольшего или наименьшего значения функции». Компьютерный журнал. 3 (3): 175–184. Дои:10.1093 / comjnl / 3.3.175. ISSN 0010-4620.

[2] Симионеску, П.А. (2014). Инструменты компьютерного построения графиков и моделирования для пользователей AutoCAD (1-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4822-5290-3.

[3] Dixon, L.C.W .; Миллс, Д. Дж. (1994). «Влияние ошибок округления на метод переменной метрики». Журнал теории оптимизации и приложений. 80: 175–179. Дои:10.1007 / BF02196600.

[4] «Обобщенная функция Розенброка». Получено 2008-09-16.

[kok2009-5] а ^б Кок, Шальк; Сандрок, Карл (2009). «Определение местоположения и характеристики стационарных точек расширенной функции Розенброка». Эволюционные вычисления. 17 (3): 437–53. Дои:10.1162 / evco.2009.17.3.437. HDL:2263/13845. PMID 19708775.

[1]

[2]

[3]

[4]

[5]