Аффинная алгебра Ли - Affine Lie algebra
В математика, аффинная алгебра Ли является бесконечномерным Алгебра Ли который построен каноническим образом из конечномерного простая алгебра Ли. Это Алгебра Каца – Муди для чего обобщенная матрица Картана положительно полуопределен и имеет коранг 1. С чисто математической точки зрения аффинные алгебры Ли интересны тем, что их теория представлений, как теория представлений конечномерных, полупростые алгебры Ли гораздо лучше изучен, чем общие алгебры Каца – Муди. По наблюдениям Виктор Кац, то формула символов для представлений аффинных алгебр Ли влечет некоторые комбинаторные тождества, Личности Макдональда.
Аффинные алгебры Ли играют важную роль в теория струн и двумерная конформная теория поля из-за способа их построения: начиная с простой алгебры Ли , считается алгебра петель, , образованный -значные функции на окружности (интерпретируемой как замкнутая струна) с поточечным коммутатором. Аффинная алгебра Ли получается добавлением одного дополнительного измерения к алгебре петель и изменением коммутатора нетривиальным способом, который физики называют квантовая аномалия (в этом случае аномалия Модель WZW ) и математики центральное расширение. В более общем смысле, если σ - автоморфизм простой алгебры Ли связанный с автоморфизмом его Диаграмма Дынкина, то алгебра скрученных петель состоит из -значные функции ж на прямой, удовлетворяющие условию скрученной периодичности f (x + 2π) = σ f (x). Их центральные продолжения - это в точности скрученные аффинные алгебры Ли. Точка зрения теории струн помогает понять многие глубокие свойства аффинных алгебр Ли, такие как тот факт, что символы их представлений трансформируются между собой под действием модульная группа.
Аффинные алгебры Ли из простых алгебр Ли
Определение
Если - конечномерная простая алгебра Ли, соответствующая аффинная алгебра Ли построен как центральное расширение бесконечномерной алгебры Ли , с одномерным центром Как векторное пространство
куда комплексное векторное пространство Полиномы Лорана в неопределенном т. Скобка Ли определяется формулой
для всех и , куда скобка Ли в алгебре Ли и это Форма Картана-убийства на
Аффинная алгебра Ли, соответствующая конечномерной полупростой алгебре Ли, является прямой суммой аффинных алгебр Ли, соответствующих ее простым слагаемым. Существует выдающийся вывод аффинной алгебры Ли, определяемый формулой
Соответствующие аффинная алгебра Каца-Муди определяется добавлением дополнительного генератора d удовлетворение [d, A] = δ (A) (а полупрямой продукт ).
Построение диаграмм Дынкина
В Диаграмма Дынкина каждой аффинной алгебры Ли состоит из соответствующей простой алгебры Ли плюс дополнительный узел, который соответствует сложению мнимого корня. Конечно, такой узел не может быть присоединен к диаграмме Дынкина в каком-либо месте, но для каждой простой алгебры Ли существует количество возможных присоединений, равное мощности группы внешние автоморфизмы алгебры Ли. В частности, эта группа всегда содержит единичный элемент, и соответствующая аффинная алгебра Ли называется раскрученный аффинная алгебра Ли. Когда простая алгебра допускает автоморфизмы, которые не являются внутренними автоморфизмами, можно получить другие диаграммы Дынкина, и они соответствуют скрученный аффинные алгебры Ли.
 Набор расширенных (раскрученных) аффинных диаграмм Дынкина с добавленными узлами зеленого цвета | 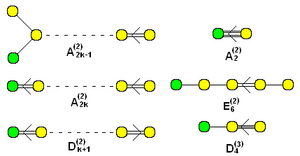 «Скрученные» аффинные формы обозначаются верхним индексом (2) или (3). (k количество узлов в графе) |
Классификация центральных пристроек
Присоединение лишнего узла к диаграмме Дынкина соответствующей простой алгебры Ли соответствует следующей конструкции. Аффинную алгебру Ли всегда можно построить как центральное расширение алгебры петель соответствующей простой алгебры Ли. Если вместо этого кто-то хочет начать с полупростой алгебры Ли, то нужно центрально расширить на число элементов, равное количеству простых компонентов полупростой алгебры. В физике вместо этого часто рассматривают прямую сумму полупростой алгебры и абелевой алгебры . В этом случае также необходимо добавить п другие центральные элементы для п абелевы генераторы.
Вторая целая когомология группы петель соответствующей простой компактной группы Ли изоморфна целым числам. Центральные расширения аффинной группы Ли с помощью одного образующего - это топологически круговые расслоения над этой группой свободных петель, которые классифицируются двумя классами, известными как первые Черн класс из расслоение. Следовательно, центральные расширения аффинной группы Ли классифицируются одним параметром k который называется уровень в физической литературе, где он впервые появился. Унитарные представления со старшим весом аффинных компактных групп существуют только тогда, когда k натуральное число. В более общем смысле, если рассматривать полупростую алгебру, для каждого простого компонента существует центральный заряд.
Теория представлений
В теория представлений для аффинных алгебр Ли обычно разрабатывается с использованием Модули Verma. Как и в случае полупростых алгебр Ли, их можно получить как модули наибольшего веса. Нет конечномерных представлений; это следует из того, что нулевые векторы конечномерного модуля Верма обязательно равны нулю; тогда как для аффинных алгебр Ли - нет. Грубо говоря, это следует потому, что Форма убийства является лоренцианским в направления, таким образом иногда называются «координатами светового конуса» на строке. "Радиально упорядоченный" текущий оператор продукты можно понимать как временные нормально заказанный принимая с времяподобное направление по струне лист мира и пространственное направление.
Группа Вейля и персонажи
В Группа Вейля аффинной алгебры Ли можно записать как полупрямой продукт группы Вейля алгебры нулевых мод (алгебры Ли, используемой для определения алгебра петель ) и решетка корора.
В Формула характера Вейля из алгебраические персонажи аффинных алгебр Ли обобщается на Формула характера Вейля-Каца. Из них следует ряд интересных построений. Можно построить обобщения Тета-функция Якоби. Эти тета-функции преобразуются под действием модульная группа. Обычные тождества знаменателя полупростых алгебр Ли также являются обобщением; потому что символы могут быть написаны как "деформации" или q-аналоги наивысших весов, это привело ко многим новым комбинаторным тождествам, включая многие ранее неизвестные тождества для Функция Дедекинда эта. Эти обобщения можно рассматривать как практический пример Программа Langlands.
Приложения
Из-за Строительство Сугавара универсальная обертывающая алгебра любой аффинной алгебры Ли имеет Алгебра Вирасоро как подалгебра. Это позволяет аффинным алгебрам Ли служить алгебрами симметрий конформные теории поля Такие как Модели WZW или смежные модели. Как следствие, аффинные алгебры Ли также появляются в описании мирового листа теория струн.
Рекомендации
- Di Francesco, P .; Mathieu, P .; Сенешаль, Д. (1997), Конформная теория поля, Springer-Verlag, ISBN 0-387-94785-X
- Фукс, Юрген (1992), Аффинные алгебры Ли и квантовые группы, Издательство Кембриджского университета, ISBN 0-521-48412-X
- Годдард, Питер; Олив, Дэвид (1988), Алгебры Каца-Муди и Вирасоро: переиздание для физиков, Продвинутая серия по математической физике, 3, World Scientific, ISBN 9971-5-0419-7
- Кац Виктор (1990), Бесконечномерные алгебры Ли (3-е изд.), Cambridge University Press, ISBN 0-521-46693-8
- Коно, Тошитаке (1998), Конформная теория поля и топология, Американское математическое общество, ISBN 0-8218-2130-X
- Прессли, Эндрю; Сигал, Грэм (1986), Группы петель, Издательство Оксфордского университета, ISBN 0-19-853535-X





![{ Displaystyle { mathfrak {g}} otimes mathbb { mathbb {C}} [т, т ^ {- 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ffdf6ad5fdfdf601af98210f181594d5f7349b1)

![{ displaystyle { widehat { mathfrak {g}}} = { mathfrak {g}} otimes mathbb { mathbb {C}} [t, t ^ {- 1}] oplus mathbb { mathbb {C}} c,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/635a8df249d1af8333a3d01c61a53cebfcb48c66)
![{ Displaystyle mathbb { mathbb {C}} [т, т ^ {- 1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24d3c75900023b6d276e960dc13a9858bb2efd13)
![[a otimes t ^ n + alpha c, b otimes t ^ m + beta c] = [a, b] otimes t ^ {n + m} + langle a | b rangle n delta_ {m + n, 0} c](https://wikimedia.org/api/rest_v1/media/math/render/svg/845b805b2d30f8eff9530c514eb2faf8a76f651c)


![[а, б]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)








