W функция Ламберта - Lambert W function
В математика, то Ламберт W функция, также называемый омега-функция или логарифм продукта, это многозначная функция, а именно ветви из обратное отношение функции ж(ш) = мыш, где ш есть ли комплексное число и еш это экспоненциальная функция.
Для каждого целого числа k есть одна ветвь, обозначенная Wk(z), которая является комплексной функцией одного сложного аргумента. W0 известен как главный филиал. Эти функции обладают следующим свойством: если z и ш - любые комплексные числа, то
выполняется тогда и только тогда, когда
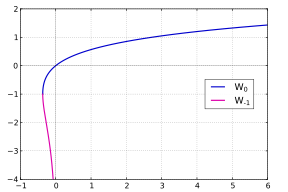
При работе только с действительными числами две ветви W0 и W−1 достаточно: для действительных чисел Икс и у уравнение
можно решить для у только если Икс ≥ −1/е; мы получаем у = W0(Икс) если Икс ≥ 0 и два значения у = W0(Икс) и у = W−1(Икс) если −1/е ≤ Икс < 0.
Ламберт W отношение не может быть выражено в терминах элементарные функции.[1] Это полезно в комбинаторика, например, при перечислении деревья. Его можно использовать для решения различных уравнений, включающих экспоненты (например, максимумы Планк, Бозе-Эйнштейн, и Ферми – Дирак распределений), а также встречается в решении дифференциальные уравнения с запаздыванием, такие как у′(т) = а у(т − 1). В биохимия, и в частности кинетика ферментов, открытое решение для анализа кинетики динамики Кинетика Михаэлиса – Ментен описывается в терминах Ламберта W функция.
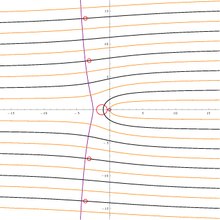
 Главный филиал Ламберта W функция в комплексной плоскости. Обратите внимание срезанная ветка вдоль отрицательной действительной оси, заканчиваясь в −1/е. На этой картинке оттенок точки z определяется аргумент из W(z), а яркость абсолютная величина из W(z).
Главный филиал Ламберта W функция в комплексной плоскости. Обратите внимание срезанная ветка вдоль отрицательной действительной оси, заканчиваясь в −1/е. На этой картинке оттенок точки z определяется аргумент из W(z), а яркость абсолютная величина из W(z).

Терминология
Ламберт W функция названа в честь Иоганн Генрих Ламберт. Главный филиал W0 обозначается Wp в Электронная библиотека математических функций, и филиал W−1 обозначается Wm Там.
Выбранное здесь обозначение (с W0 и W−1) следует канонической ссылке на Ламберт W функция Корлесса, Гонне, Хэра, Джеффри и Knuth.[2]
Название «логарифм продукта» можно понимать так: Поскольку обратная функция из ж(ш) = еш называется логарифм, имеет смысл вызвать обратную функцию товар мыш как «логарифм продукта». Это связано с Постоянная омега, что равно W0(1).
История
Ламберт первым рассмотрел родственные Трансцендентное уравнение Ламберта в 1758 г.,[3] что привело к статье Леонард Эйлер в 1783 г.[4] который обсуждал особый случай мыш.
Рассматриваемая функция Ламберта была
Эйлер преобразовал это уравнение к виду
Оба автора получили решение ряда своих уравнений.
Решив это уравнение, Эйлер рассмотрел случай а = б. Взяв пределы, он вывел уравнение
Затем он положил а = 1 и получили решение сходящегося ряда для полученного уравнения, выражающее Икс с точки зрения c.
После взятия производных по Икс После некоторых манипуляций получен стандартный вид функции Ламберта.
В 1993 году, когда стало известно, что Ламберт W функция обеспечивает точное решение квантово-механической двухъямная модель дельта-функции Дирака для равных зарядов - фундаментальная проблема физики - Корлесс и разработчики Клен Система компьютерной алгебры произвела поиск в библиотеке и обнаружила, что эта функция является повсеместной по своей природе.[2][5]
Другой пример, где встречается эта функция, находится в Кинетика Михаэлиса – Ментен.
Хотя это было фольклорное знание, что Ламберт W Функция не может быть выражена через элементарные (лиувиллевы) функции, первое опубликованное доказательство появилось только в 2008 году.[6]
Элементарные свойства, ветви и ассортимент
Существует счетное множество ветвей W функция, обозначаемая Wk(z), для целого числа k; W0(z) являясь основным (или главным) филиалом. W0(z) определено для всех комплексных чисел z в то время как Wk(z) с участием k ≠ 0 определено для всех ненулевых z. У нас есть W0(0) = 0 и Wk(z) = −∞ для всех k ≠ 0.
Точка ветвления для основной ветви находится в z = −1/е, с разрезом ветви, доходящим до −∞ вдоль отрицательной действительной оси. Этот разрез отделяет основную ветвь от двух ветвей. W−1 и W1. Во всех отраслях Wk с участием k ≠ 0, есть точка ветвления в z = 0 и ветвь, разрезанная по всей отрицательной действительной оси.
Функции Wk(z), k ∈ Z все инъективный и их диапазоны не пересекаются. Диапазон всей многозначной функции W - комплексная плоскость. Изображение действительной оси представляет собой объединение действительной оси и квадратик Гиппия, параметрическая кривая ш = −т детская кроватка т + Это.
Обратный

График диапазона выше также очерчивает области на комплексной плоскости, где простая обратная связь ' правда. ж=зеz означает, что существует п такой, что , где п будет зависеть от стоимости z. Значение целого числа п резко изменится, когда зеz находится на срезе ветки что будет означать, что зеz ≤ 0, кроме где это будет зеz ≤ -1/е.
Определить где Икс и у настоящие. Выражая еz в полярных координатах видно, что:
Для , срезанная ветка для будет неположительной действительной осью, так что:
и
Для , срезанная ветка для будет реальная ось с так что неравенство становится:
Внутри областей, ограниченных указанным выше, скачкообразных изменений и в этих регионах будет указано, где W функция просто обратима: т.е. .
Исчисление
Производная
От неявное дифференцирование, можно показать, что все ветви W удовлетворить дифференциальное уравнение
(W не является дифференцируемый для z = −1/е.) Как следствие, получаем следующую формулу для производной от W:
Используя личность еW(z) = z/W(z), получаем следующую эквивалентную формулу:
В начале мы имеем
Первообразный
Функция W(Икс), и многие выражения, включающие W(Икс), может быть интегрированный с использованием замена ш = W(Икс), т.е. Икс = мыш:
(Последнее уравнение чаще встречается в литературе, но не выполняется при Икс = 0). Одно из следствий этого (используя тот факт, что W0(е) = 1) - это тождество
Асимптотические разложения
В Серия Тейлор из W0 около 0 можно найти с помощью Теорема обращения Лагранжа и дается
В радиус схождения является 1/е, как видно из тест соотношения. Функция, определяемая этой серией, может быть расширена до голоморфная функция определен на всех комплексных числах с срезанная ветка вдоль интервал (−∞, −1/е]; эта голоморфная функция определяет главный филиал Ламберта W функция.
Для больших значений Икс, W0 асимптотичен
где L1 = ln Икс, L2 = ln ln Икс, и [л + м
л + 1] неотрицательный Число Стирлинга первого рода.[2] Сохраняя только первые два условия расширения,
Другая настоящая ветка, W−1, определенный в интервале [−1/е, 0), имеет приближение того же вида, что и Икс стремится к нулю, в этом случае L1 = ln (-Икс) и L2 = ln (−ln (-Икс)).[2]
Показано[7] справедлива следующая оценка (оценка сверху только для Икс ≥ е):
В 2013 году было доказано[8] что филиал W−1 можно ограничить следующим образом:
Целочисленные и комплексные степени
Целочисленные степени W0 также признать простой Тейлор (или Лоран ) разложения в нуле:
В более общем плане для р ∈ ℤ, то Формула обращения Лагранжа дает
что в общем случае является рядом Лорана порядка р. Эквивалентно последнее может быть записано в форме разложения Тейлора степеней W0(Икс) / Икс:
что справедливо для любого р ∈ ℂ и |Икс| < 1/е.
Идентичности

Из определения следует несколько идентичностей:
Обратите внимание, что, поскольку ж(Икс) = xeИкс не является инъективный, не всегда W(ж(Икс)) = Икс, как и в случае с обратные тригонометрические функции. Для фиксированных Икс < 0 и Икс ≠ −1, уравнение xeИкс = выу имеет два решения в у, один из которых, конечно, у = Икс. Тогда для я = 0 и Икс < −1, а также для я = −1 и Икс ∈ (−1, 0), у = Wя(xeИкс) другое решение.
Некоторые другие личности:[9]
- (который может быть расширен на другие п и Икс если выбрана правильная ветка).
Подстановка −ln Икс в определении:
С повторной экспонентой Эйлера час(Икс):
Особые ценности
Для любого ненулевого алгебраическое число Икс, W(Икс) это трансцендентное число. Действительно, если W(Икс) равно нулю, то Икс также должен быть равен нулю, и если W(Икс) отличен от нуля и алгебраичен, то по Теорема Линдемана – Вейерштрасса, еW(Икс) должно быть трансцендентным, подразумевая, что Икс = W(Икс)еW(Икс) также должно быть трансцендентным.
Ниже приведены особые значения основной ветви:
- (в омега-константа ).
Представления
Основная ветвь функции Ламберта может быть представлена собственным интегралом благодаря Пуассону:[11]
В более широком смысле −1/е ≤ Икс ≤ е, значительно более простое представление найдено Мезо:[12]
Следующее непрерывная дробь представление справедливо и для главной ветви:[13]
Кроме того, если |W(z)| < 1:[14]
В свою очередь, если |W(z)| > е, тогда
Другие формулы
Определенные интегралы
Существует несколько полезных определенных интегральных формул, включающих главную ветвь W функции, в том числе следующие:
Первую личность можно найти, написав Гауссов интеграл в полярные координаты.
Вторую идентичность можно получить, сделав замену ты = W(Икс), который дает
Таким образом
Третья идентичность может быть получена из второй путем замены ты = Икс−2 и первое также может быть получено из третьего путем замены z = 1/√2 загар Икс.
Кроме z вдоль среза ветки (−∞, −1/е] (где интеграл не сходится) главная ветвь ламбертовского W функция может быть вычислена с помощью следующего интеграла:[15]
где два интегральных выражения эквивалентны из-за симметрии подынтегрального выражения.
Неопределенные интегралы
Приложения
Решение уравнений
Ламберт W Функция используется для решения уравнений, в которых неизвестная величина встречается как в основании, так и в показателе степени, или как внутри, так и вне логарифма. Стратегия состоит в том, чтобы преобразовать такое уравнение в одну из форм зеz = ш а затем решить для z. с использованием W функция.
Например, уравнение
(где Икс неизвестное действительное число) можно решить, переписав его как
Это последнее уравнение имеет желаемую форму, а решения для действительного x:
и поэтому:
Как правило, решение
является:
где а, б, и c комплексные константы, с б и c не равно нулю, и W функция имеет любой целочисленный порядок.
Вязкие потоки
Фронты и отложения зернистых и селевых потоков, а также фронты вязких флюидов в природных явлениях и в лабораторных экспериментах можно описать с помощью омега-функции Ламберта-Эйлера следующим образом:
где ЧАС(Икс) высота селевого потока, Икс положение канала ниже по потоку, L - параметр единой модели, состоящий из нескольких физических и геометрических параметров потока, высоты потока и градиента гидравлического давления.
В поток трубы, функция Ламберта W является частью явной формулировки Уравнение Колбрука для поиска Коэффициент трения Дарси. Этот коэффициент используется для определения падения давления на прямом участке трубы, когда расход бурный.[16]
Нейровизуализация
Ламберт W Функция была использована в области нейровизуализации для связи изменений мозгового кровотока и потребления кислорода в вокселе мозга с соответствующим сигналом, зависимым от уровня оксигенации крови (ЖИРНЫЙ).[17]
Химическая инженерия
Ламберт W Функция была использована в области химической инженерии для моделирования толщины пористой электродной пленки в стеклоуглерод на основании суперконденсатор для электрохимического накопления энергии. Ламберт W Функция оказалась точным решением для процесса термической активации в газовой фазе, где рост углеродной пленки и горение одной и той же пленки конкурируют друг с другом.[18][19]
Материаловедение
Ламберт W функция использовалась в области эпитаксиальный рост пленки для определения критического вывих начальная толщина пленки. Это расчетная толщина эпитаксиальной пленки, при которой в соответствии с термодинамическими принципами в пленке будут развиваться кристаллографические дислокации, чтобы минимизировать запасенную в пленках упругую энергию. До применения Ламберта W для этой задачи критическая толщина должна быть определена путем решения неявного уравнения. Ламберт W с легкостью превращает его в явное уравнение для аналитической обработки.[20]
Пористая среда
Ламберт W Функция была использована в области течения жидкости в пористой среде для моделирования наклона границы раздела двух гравитационно разделенных жидкостей в однородном наклонном пористом слое постоянного падения и толщины, где более тяжелая жидкость, нагнетаемая в нижний конец, вытесняет более легкую. жидкость, которая добывается с той же скоростью из верхнего конца. Основная ветвь решения соответствует стабильным смещениям, а ветвь -1 применяется, если смещение нестабильно, когда более тяжелая жидкость течет под более легкой.[21]
Числа Бернулли и род Тодда
Уравнение (связанное с производящими функциями Числа Бернулли и Род Тоддов ):
может быть решена с помощью двух реальных ветвей W0 и W−1:
Это приложение показывает, что разница ветвей W функция может использоваться для решения других трансцендентных уравнений.[22]
Статистика
Центроид набора гистограмм, определенных относительно симметризованной дивергенции Кульбака – Лейблера (также называемой дивергенцией Джеффриса [23]) имеет замкнутый вид с использованием формулы Ламберта W функция.[24]
Точные решения уравнения Шредингера
Ламберт W функция появляется в квантово-механическом потенциале, который дает пятый - рядом с гармоническим осциллятором плюс центробежный, кулоновским плюс обратным квадратом, Морзе и потенциал обратного квадратного корня - точное решение стационарного одномерного уравнения Шредингера в терминах вырожденных гипергеометрических функций. Потенциал задается как
Особенность решения состоит в том, что каждое из двух фундаментальных решений, составляющих общее решение уравнения Шредингера, задается комбинацией двух конфлюэнтных гипергеометрических функций аргумента, пропорционального[25]
Ламберт W функция также входит в точное решение для энергии связанного состояния одномерного уравнения Шредингера с Двойной дельта-потенциал.
Точные решения вакуумных уравнений Эйнштейна
в Метрика Шварцшильда решение вакуумных уравнений Эйнштейна, W функция необходима для перехода от Координаты Эддингтона – Финкельштейна в координаты Шварцшильда. По этой причине он также появляется в конструкции Координаты Крускала – Секереса.
Резонансы потенциала дельта-оболочки
S-волновые резонансы потенциала дельта-оболочки могут быть точно записаны в терминах Ламберта W функция.[26]
Термодинамическое равновесие
Если в реакции участвуют реагенты и продукты, имеющие тепловые мощности постоянные с температурой, то константа равновесия K подчиняется
для некоторых констант а, б, и c. Когда c (равно ΔCп/р) не равно нулю, мы можем найти значение или значения Т где K равно заданному значению следующим образом, где мы используем L для пер Т.
Если а и c имеют один и тот же знак, то будет либо два решения, либо ни одного (или одно, если аргумент W точно −1/е). (Верхнее решение может не иметь отношения.) Если они имеют противоположные знаки, будет одно решение.
AdS / CFT корреспонденция
Классические конечномерные поправки к дисперсионным соотношениям гигантские магноны, одиночные шипы и Струны GKP можно выразить через формулу Ламберта W функция.[27][28]
Эпидемиология
в т → ∞ предел Модель SIR, соотношение восприимчивых и выздоровевших людей имеет решение в терминах Ламберта W функция.[29]
Определение времени полета снаряда
Общее время полета снаряда, который испытывает сопротивление воздуха, пропорциональное его скорости. можно определить в точном виде с помощью метода Ламберта W функция.
Обобщения
Стандартный Ламберт W функция выражает точные решения трансцендентно-алгебраический уравнения (в Икс) формы:
(1)
где а0, c и р реальные константы. Решение
Обобщения Ламберта W функция[30][31][32] включают:
- Приложение к общая теория относительности и квантовая механика (квантовая гравитация ) в более низких измерениях, фактически ссылка (неизвестно до 2007 г.[33]) между этими двумя областями, где правая часть (1) заменяется квадратичным многочленом от Икс:
(2)
- где р1 и р2 - действительные различные константы, корни квадратичного многочлена. Здесь решение - это функция с единственным аргументом Икс но такие термины, как ря и а0 параметры этой функции. В этом отношении обобщение напоминает гипергеометрический функция и Мейер г функция но он принадлежит другому класс функций. Когда р1 = р2, обе стороны (2) можно разложить на множители и свести к (1) и, таким образом, решение сводится к решению стандартного W функция. Уравнение (2) выражает уравнение, определяющее дилатон поле, из которого выводится метрика р = Т или линейный задача двух тел гравитации в 1 + 1 измерениях (одно пространственное измерение и одно временное измерение) для случая неравных масс покоя, а также собственные энергии квантово-механических двухъямная модель дельта-функции Дирака для неравный заряды в одном измерении.
- Аналитические решения собственных энергий частного случая квантовой механики. проблема трех тел, а именно (трехмерный) молекула водорода-ион.[34] Здесь правая часть (1) заменяется отношением полиномов бесконечного порядка от Икс:
(3)
- где ря и sя различные действительные константы и Икс является функцией собственной энергии и межъядерного расстояния р. Уравнение (3) с его частными падежами, выраженными в (1) и (2) относится к большому классу дифференциальные уравнения с запаздыванием. Г. Х. Харди понятие "ложной производной" дает точные множественные корни частным случаям (3).[35]
Приложения Ламберта W функции в фундаментальных физических задачах не исчерпываются даже для стандартного случая, выраженного в (1), как это было недавно замечено в районе атомная, молекулярная и оптическая физика.[36]
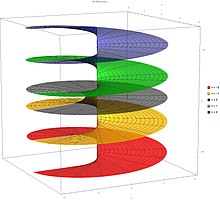
Сюжеты
- Сюжеты Ламберта W функция на комплексной плоскости

z = Re (W0(Икс + иу))

z = Im (W0(Икс + иу))

z = |W0(Икс + иу)|

Наложение трех предыдущих сюжетов
Числовая оценка
В W функция может быть аппроксимирована с помощью Метод Ньютона, с последовательными приближениями к ш = W(z) (так z = мыш) будучи
В W функция также может быть аппроксимирована с помощью Метод Галлея,
приведено в Corless et al.[2] вычислить W.
Программного обеспечения
Ламберт W функция реализована какLambertW в клене, Lambertw в GP (и glambertW в PARI ), Lambertw в Matlab,[37] также Lambertw в Октава с specfun пакет, как lambert_w в Максима,[38] так как ProductLog (с тихим псевдонимом LambertW) в Mathematica,[39] так как Lambertw в Python странный специальный пакет функций,[40] так как LambertW в Perl теория модуль[41] и в качестве gsl_sf_lambert_W0, gsl_sf_lambert_Wm1 функции в специальные функции раздел Научная библиотека GNU (GSL). в Библиотеки Boost C ++, звонки lambert_w0, lambert_wm1, lambert_w0_prime, и lambert_wm1_prime. В р, Ламберт W функция реализована как lambertW0 и lambertWm1 функции в lamW пакет.[42]
Код на C ++ для всех ветвей комплекса Ламберта W Функция доступна на домашней странице Иштвана Мезо.[43]
Смотрите также
- Омега-функция Райта
- Ламберта трехчленное уравнение
- Теорема обращения Лагранжа
- Экспериментальная математика
- Метод голштинской селедки
- р = Т модель
- Росс π лемма
Заметки
- ^ Чоу, Тимоти Ю. (1999), «Что такое число в закрытой форме?», Американский математический ежемесячный журнал, 106 (5): 440–448, arXiv:математика / 9805045, Дои:10.2307/2589148, JSTOR 2589148, Г-Н 1699262.
- ^ а б c d е Corless, R.M .; Gonnet, G.H .; Hare, D. E. G .; Джеффри, Д. Дж .; Кнут, Д. Э. (1996). "На Ламберте W функция " (PostScript). Достижения в вычислительной математике. 5: 329–359. arXiv:1809.07369. Дои:10.1007 / BF02124750. S2CID 29028411.
- ^ Ламберт Дж. Х., "Observationes variae в матесин пурам", Acta Helveticae физико-математико-анатомо-ботанико-медика, Band III, 128–168, 1758.
- ^ Эйлер, Л. "Из серии Lambertina Plurimisque eius insignibus proprietatibus". Acta Acad. Научный. Петрополь. 2, 29–51, 1783. Перепечатано в Euler, L. Опера Омния, Серия Прима, Том. 6. Алгебраические комментарии. Лейпциг, Германия: Teubner, стр. 350–369, 1921.
- ^ Corless, R.M .; Gonnet, G.H .; Hare, D. E. G .; Джеффри, Д. Дж. (1993). "Ламберта W функция в Maple ". Технический бюллетень Maple. 9: 12–22. CiteSeerX 10.1.1.33.2556.
- ^ Бронштейн, Мануэль; Корлесс, Роберт М .; Давенпорт, Джеймс Х .; Джеффри, Д.Дж. (2008). «Алгебраические свойства Ламберта W функция из результата Розенлихта и Лиувилля ". Интегральные преобразования и специальные функции. 19 (10): 709–712. Дои:10.1080/10652460802332342.
- ^ А. Хоорфар, М. Хассани, Неравенства по Ламберту W Функция и функция сверхмощности, JIPAM, том 9, выпуск 2, статья 51. 2008 г.
- ^ Чатзигеоргиу, И. (2013). «Границы функции Ламберта и их применение для анализа сбоев взаимодействия пользователей». Письма по коммуникациям IEEE. 17 (8): 1505–1508. arXiv:1601.04895. Дои:10.1109 / LCOMM.2013.070113.130972. S2CID 10062685.
- ^ «Функция Ламберта: Тождества (формула 01.31.17.0001)».
- ^ «W-функция Ламберта».
- ^ Финч, С. Р. (2003). Математические константы. Издательство Кембриджского университета. п. 450.
- ^ Иштван, Мезо. "Интегральное представление основной ветви Ламберта W функция ". Получено 7 ноября 2017.
- ^ Дубинов, А.Е .; Дубинова, И. Д .; Сайков, С. К. (2006). Ламберт W Функция и ее приложения к математическим задачам физики.. РФЯЦ-ВНИИЭФ. п. 53.
- ^ Роберт М., Корлесс; Дэвид Дж., Джеффри; Дональд Э., Кнут (1997). Последовательность серий для Ламберта W функция. Труды Международного симпозиума 1997 г. по символическим и алгебраическим вычислениям. С. 197–204. Дои:10.1145/258726.258783. ISBN 978-0897918756. S2CID 6274712.
- ^ "Ламберт W Функция ". Исследовательский центр компьютерной алгебры Онтарио.
- ^ Подробнее, А. А. (2006). «Аналитические решения для уравнения Коулбрука и Уайта и падения давления в потоке идеального газа в трубах». Химическая инженерия. 61 (16): 5515–5519. Дои:10.1016 / j.ces.2006.04.003.
- ^ Сотеро, Роберто Ч .; Итуррия-Медина, Яссер (2011). «От сигналов, зависящих от уровня оксигенации крови (жирный шрифт), до карт температуры мозга». Бык математика биол (Представлена рукопись). 73 (11): 2731–47. Дои:10.1007 / s11538-011-9645-5. PMID 21409512. S2CID 12080132.
- ^ Браун, Артур; Вокаун, Александр; Херманс, Хайнц-Гюнтер (2003). «Аналитическое решение проблемы роста с двумя подвижными границами». Математическая модель приложения. 27 (1): 47–52. Дои:10.1016 / S0307-904X (02) 00085-9.
- ^ Браун, Артур; Бэрч, Мартин; Шнайдер, Бернхард; Кетц, Рюдигер (2000). «Модель роста пленки в образцах с двумя движущимися границами - применение и расширение модели непрореагировавшего ядра». Chem Eng Sci. 55 (22): 5273–5282. Дои:10.1016 / S0009-2509 (00) 00143-3.
- ^ Браун, Артур; Бриггс, Кейт М .; Боени, Питер (2003). "Аналитическое решение критической толщины образования дислокаций Мэтьюза и Блэксли эпитаксиально выращенных тонких пленок". Рост J Cryst. 241 (1–2): 231–234. Bibcode:2002JCrGr.241..231B. Дои:10.1016 / S0022-0248 (02) 00941-7.
- ^ Колла, Пьетро (2014). «Новый аналитический метод движения двухфазной границы раздела в наклонной пористой среде». ТРУДЫ, Тридцать восьмой семинар по разработке геотермальных резервуаров, Стэнфордский университет. SGP-TR-202.([1] )
- ^ Д. Дж. Джеффри и Дж. Э. Янковски, "Различия ветвей и Ламберт". W"
- ^ Флавия-Корина Митрой-Симеонидис, Ион Ангел, Сигеру Фуруичи (2019). «Кодировки для расчета перестановочной гипоэнтропии и их приложения к натурным данным о пожаре в отсеке». Acta Technica Napocensis. 62, IV: 607-616.CS1 maint: несколько имен: список авторов (ссылка на сайт)
- ^ Ф. Нильсен, "Центроиды Джеффриса: выражение в закрытой форме для положительных гистограмм и гарантированное точное приближение для частотных гистограмм"
- ^ A.M. Ишханян, "Ламберт" W барьер - точно решаемый конфлюэнтный гипергеометрический потенциал ».
- ^ де ла Мадрид, Р. (2017). «Численный расчет ширин распада, констант распада и энергетических спектров распада резонансов потенциала дельта-оболочки». Nucl. Phys. А. 962: 24–45. arXiv:1704.00047. Bibcode:2017НуФА.962 ... 24Д. Дои:10.1016 / j.nuclphysa.2017.03.006. S2CID 119218907.
- ^ Флоратос, Эммануэль; Георгиу, Джордж; Линардопулос, Георгиос (2014). "Расширение струн GKP при большом вращении". JHEP. 2014 (3): 0180. arXiv:1311.5800. Bibcode:2014JHEP ... 03..018F. Дои:10.1007 / JHEP03 (2014) 018. S2CID 53355961.
- ^ Флоратос, Эммануэль; Линардопулос, Георгиос (2015). "Расширения гигантских магнонов и одиночных шипов с большим спином и большой обмоткой". Nucl. Phys. B. 897: 229–275. arXiv:1406.0796. Bibcode:2015НуФБ.897..229Ф. Дои:10.1016 / j.nuclphysb.2015.05.021. S2CID 118526569.
- ^ Wolfram Research, Inc. "Mathematica, Версия 12.1". Шампанское Иллинойс, 2020.
- ^ Scott, T. C .; Mann, R. B .; Мартинес II, Роберто Э. (2006). «Общая теория относительности и квантовая механика: к обобщению теории Ламберта. W Функция ». AAECC (Применимая алгебра в инженерии, коммуникации и вычислениях). 17 (1): 41–47. arXiv:math-ph / 0607011. Bibcode:2006math.ph ... 7011S. Дои:10.1007 / s00200-006-0196-1. S2CID 14664985.
- ^ Scott, T. C .; Комиссия, G .; Гротендорст, Дж. (2013). «Асимптотический ряд обобщенного Ламберта. W Функция ". SIGSAM (Специальная группа ACM по символьным и алгебраическим манипуляциям). 47 (185): 75–83. Дои:10.1145/2576802.2576804. S2CID 15370297.
- ^ Scott, T. C .; Комиссия, G .; Grotendorst, J .; Чжан, W.Z. (2014). "Числа обобщенного Ламберта W Функция ". SIGSAM. 48 (1/2): 42–56. Дои:10.1145/2644288.2644298. S2CID 15776321.
- ^ Farrugia, P. S .; Mann, R. B .; Скотт, Т. С. (2007). "N-тесная гравитация и уравнение Шредингера ». Класс. Квантовая гравитация. 24 (18): 4647–4659. arXiv:gr-qc / 0611144. Bibcode:2007CQGra..24.4647F. Дои:10.1088/0264-9381/24/18/006. S2CID 119365501.
- ^ Scott, T. C .; Обер-Фрекон, М .; Гротендорст, Дж. (2006). «Новый подход к электронным энергиям молекулярного иона водорода». Chem. Phys. 324 (2–3): 323–338. arXiv:физика / 0607081. Bibcode:2006CP .... 324..323S. CiteSeerX 10.1.1.261.9067. Дои:10.1016 / j.chemphys.2005.10.031. S2CID 623114.
- ^ Maignan, Aude; Скотт, Т. К. (2016)."Конкретизируя обобщенный Ламберт W Функция ». SIGSAM. 50 (2): 45–60. Дои:10.1145/2992274.2992275.
- ^ Scott, T. C .; Lüchow, A .; Брессанини, Д .; Морган, Дж. Д. III (2007). «Узловые поверхности собственных функций атома гелия» (PDF). Phys. Ред. А. 75 (6): 060101. Bibcode:2007PhRvA..75f0101S. Дои:10.1103 / PhysRevA.75.060101. HDL:11383/1679348.
- ^ lambertw - MATLAB
- ^ Maxima, система компьютерной алгебры
- ^ ProductLog на WolframAlpha
- ^ "Scipy.special.lambertw - Справочное руководство SciPy v0.16.1".
- ^ ntheory в MetaCPAN
- ^ Адлер, Авраам (24.04.2017), lamW: Ламберт W Функция, получено 2017-12-19
- ^ Веб-страница Иштвана Мезо
использованная литература
- Corless, R .; Gonnet, G .; Заяц, Д .; Джеффри, Д .; Кнут, Дональд (1996). "На Ламберте W функция " (PDF). Достижения в вычислительной математике. 5: 329–359. Дои:10.1007 / BF02124750. ISSN 1019-7168. S2CID 29028411. Архивировано из оригинал (PDF) на 2010-12-14. Получено 2007-03-10.
- Chapeau-Blondeau, F .; Монир, А. (2002). "Оценка Ламберта W Функция и применение для генерации обобщенного гауссовского шума с показателем 1/2 " (PDF). IEEE Trans. Сигнальный процесс. 50 (9). Дои:10.1109 / TSP.2002.801912. Архивировано из оригинал (PDF) на 2012-03-28. Получено 2004-03-10.
- Фрэнсис; и другие. (2000). «Количественная общая теория периодического дыхания». Тираж. 102 (18): 2214–21. CiteSeerX 10.1.1.505.7194. Дои:10.1161 / 01.cir.102.18.2214. PMID 11056095. S2CID 14410926. (Функция Ламберта используется для решения дифференциальной динамики задержки при заболеваниях человека.)
- Хейс, Б. (2005). "Зачем W?" (PDF). Американский ученый. 93 (2): 104–108. Дои:10.1511/2005.2.104.
- Рой, Р .; Олвер, Ф. В. Дж. (2010), "Ламберт W функция ", в Олвер, Фрэнк В. Дж.; Lozier, Daniel M .; Бойсверт, Рональд Ф .; Кларк, Чарльз В. (ред.), Справочник NIST по математическим функциям, Издательство Кембриджского университета, ISBN 978-0-521-19225-5, Г-Н 2723248
- Стюарт, Шон М. (2005). "Новая элементарная функция для нашей учебной программы?" (PDF). Австралийский старший математический журнал. 19 (2): 8–26. ISSN 0819-4564. ЭРИК EJ720055. Сложить резюме.
- Веберик, Д., "Развлекается с Ламбертом" W(Икс) Функция "arXiv: 1003.1628 (2010); Веберич, Д. (2012). "Ламберт W функция для приложений в физике ». Компьютерная физика Коммуникации. 183 (12): 2622–2628. arXiv:1209.0735. Bibcode:2012CoPhC.183.2622V. Дои:10.1016 / j.cpc.2012.07.008. S2CID 315088.
- Чатзигеоргиу, И. (2013). «Границы функции Ламберта и их применение для анализа сбоев взаимодействия пользователей». Письма по коммуникациям IEEE. 17 (8): 1505–1508. arXiv:1601.04895. Дои:10.1109 / LCOMM.2013.070113.130972. S2CID 10062685.
















![{ displaystyle W [п, ze ^ {z}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fb4be5264a023f670dd1e4d4db4fbbffa4b51573)











![{ displaystyle { begin {align} W_ {0} (x) & = L_ {1} -L_ {2} + { frac {L_ {2}} {L_ {1}}} + { frac {L_ {2} left (-2 + L_ {2} right)} {2L_ {1} ^ {2}}} + { frac {L_ {2} left (6-9L_ {2} + 2L_ {2 } ^ {2} right)} {6L_ {1} ^ {3}}} + { frac {L_ {2} left (-12 + 36L_ {2} -22L_ {2} ^ {2} + 3L_ {2} ^ {3} right)} {12L_ {1} ^ {4}}} + cdots [5pt] & = L_ {1} -L_ {2} + sum _ {l = 0} ^ { infty} sum _ {m = 1} ^ { infty} { frac {(-1) ^ {l} left [{ begin {smallmatrix} l + m l + 1 end { smallmatrix}} right]} {m!}} L_ {1} ^ {- lm} L_ {2} ^ {m}, end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5e7cb8d231b7fabe03c2fc5d8845d1c9e18f467)







![{ displaystyle { begin {align} & W (x) cdot e ^ {W (x)} = x, quad { text {, следовательно:}} [5pt] & e ^ {W (x)} = { frac {x} {W (x)}}, qquad e ^ {- W (x)} = { frac {W (x)} {x}}, qquad e ^ {nW (x)} = left ({ frac {x} {W (x)}} right) ^ {n}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aec6ece137d76f1a83fb80dc6526314fc5fc5f5f)



![{ displaystyle { begin {align} & W (x) = ln { frac {x} {W (x)}} && { text {for}} x geq - { frac {1} {e} }, [5pt] & W left ({ frac {nx ^ {n}} {W left (x right) ^ {n-1}}} right) = nW (x) && { text {for}} n, x> 0 end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e834c16fb0e25cf530b84a39bdcc0bba7c75d762)

![{ displaystyle { begin {align} W_ {0} left (- { frac { ln x} {x}} right) & = - ln x & { text {for}} 0 & <x leq e, [5pt] W _ {- 1} left (- { frac { ln x} {x}} right) & = - ln x & { text {for}} x &> e. end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/108810da107aa426c8708fe1c3eaa34a2da9575e)
















![{ displaystyle { begin {align} & int _ {0} ^ { pi} W left (2 cot ^ {2} x right) sec ^ {2} x , dx = 4 { sqrt { pi}}. [5pt] & int _ {0} ^ { infty} { frac {W (x)} {x { sqrt {x}}}} , dx = 2 { sqrt {2 pi}}. [5pt] & int _ {0} ^ { infty} W left ({ frac {1} {x ^ {2}}} right) , dx = { sqrt {2 pi}}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/620694b88ee7cd156e478ea431d8234a5d210cad)
![{ displaystyle { begin {align} x & = ue ^ {u}, [5pt] { frac {dx} {du}} & = (u + 1) e ^ {u}. end {выравнивается} }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6d9f83a1f16b84fd3408ce93ce89f1165e8c455e)
![{ displaystyle { begin {align} int _ {0} ^ { infty} { frac {W (x)} {x { sqrt {x}}}} , dx & = int _ {0} ^ { infty} { frac {u} {ue ^ {u} { sqrt {ue ^ {u}}}}} (u + 1) e ^ {u} , du [5pt] & = int _ {0} ^ { infty} { frac {u + 1} { sqrt {ue ^ {u}}}} du [5pt] & = int _ {0} ^ { infty} { frac {u + 1} { sqrt {u}}} { frac {1} { sqrt {e ^ {u}}}} du [5pt] & = int _ {0} ^ { infty} u ^ { tfrac {1} {2}} e ^ {- { frac {u} {2}}} du + int _ {0} ^ { infty} u ^ {- { tfrac { 1} {2}}} e ^ {- { frac {u} {2}}} du [5pt] & = 2 int _ {0} ^ { infty} (2w) ^ { tfrac { 1} {2}} e ^ {- w} , dw + 2 int _ {0} ^ { infty} (2w) ^ {- { tfrac {1} {2}}} e ^ {- w } , dw && quad (u = 2w) [5pt] & = 2 { sqrt {2}} int _ {0} ^ { infty} w ^ { tfrac {1} {2}} e ^ {- w} , dw + { sqrt {2}} int _ {0} ^ { infty} w ^ {- { tfrac {1} {2}}} e ^ {- w} , dw [5pt] & = 2 { sqrt {2}} cdot Gamma left ({ tfrac {3} {2}} right) + { sqrt {2}} cdot Gamma left ( { tfrac {1} {2}} right) [5pt] & = 2 { sqrt {2}} left ({ tfrac {1} {2}} { sqrt { pi}} right) + { sqrt {2}} left ({ sqrt { pi}} right) [5pt] & = 2 { sqrt {2 pi}}. end {выравнивается}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f5305e2e7a64d2a0de58006823905769d3df94a)
![{ displaystyle { begin {align} W (z) & = { frac {z} {2 pi}} int _ {- pi} ^ { pi} { frac { left (1- nu cot nu right) ^ {2} + nu ^ {2}} {z + nu csc nu e ^ {- nu cot nu}}} , d nu [5pt ] & = { frac {z} { pi}} int _ {0} ^ { pi} { frac { left (1- nu cot nu right) ^ {2} + nu ^ {2}} {z + nu csc nu e ^ {- nu cot nu}}} , d nu, end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8a7e9fe45c952d8c323173de425832df114c930)
![{ displaystyle { begin {align} & int { frac {W (x)} {x}} dx = { tfrac {1} {2}} { bigl (} 1 + W (x) { bigr)} ^ {2} + C. [5pt] & int W left (Ae ^ {Bx} right) dx = { frac {1} {2B}} { bigl (} 1 + W left (Ae ^ {Bx} right) { bigr)} ^ {2} + C. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c62247f9bad14670a8dca929e0521b75e900e1c)












![{ displaystyle { begin {align} -a & = (b- ln K) T + cT ln T & = (b- ln K) e ^ {L} + cLe ^ {L} [ 5pt] - { frac {a} {c}} & = left ({ frac {b- ln K} {c}} + L right) e ^ {L} [5pt] - { frac {a} {c}} e ^ { frac {b- ln K} {c}} & = left (L + { frac {b- ln K} {c}} right) e ^ { L + { frac {b- ln K} {c}}} [5pt] L & = W left (- { frac {a} {c}} e ^ { frac {b- ln K}) {c}} right) + { frac { ln Kb} {c}} [5pt] T & = exp left (W left (- { frac {a} {c}} e ^ { frac {b- ln K} {c}} right) + { frac { ln Kb} {c}} right). end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3eb5cee9fdd7908a30ded5a772ec49f985ebaa1a)









