Гамильтонова связь - Hamiltonian constraint - Wikipedia

Для характеристики петлевой квантовой гравитации см. Гамильтонова связь LQG.

В Гамильтонова связь возникает из любой теории, допускающей Гамильтонова формулировка и является перепараметризация -инвариантный. Гамильтонова связь общая теория относительности важный нетривиальный пример.

В контексте общей теории относительности гамильтонова связь технически относится к линейная комбинация пространственного и временного диффеоморфизм ограничения, отражающие репараметризуемость теории как в пространственных, так и в временных координатах. Однако в большинстве случаев термин Гамильтонова связь зарезервировано для ограничения, которое порождает диффеоморфизмы времени.

Самый простой пример: параметризованные часы и маятниковая система.

Параметризация

В обычном представлении классическая механика кажется, что время как независимая переменная играет особую роль. Однако в этом нет необходимости. Механика может быть сформулирована для обработки временной переменной на том же основании, что и другие переменные в расширенном фазовом пространстве, путем параметризации временной (ых) переменной (переменных) в терминах общей, хотя и неуказанной переменной параметра. Переменные фазового пространства находятся на одном основании.

Мы представляем ${\displaystyle \tau }$ как нефизический параметр, обозначающий различные возможные корреляции между показаниями времени ${\displaystyle t}$ часов и удлинения ${\displaystyle x}$ маятника. ${\displaystyle \tau }$ - нефизический параметр, и для него есть много разных вариантов.

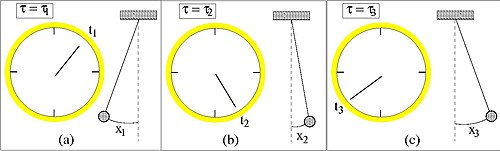
Допустим, наша система состоит из маятника, совершающего простое гармоническое движение, и часов. В то время как система может быть описана классически позицией x = x (t), где x определяется как функция времени, также можно описать ту же систему как x (${\displaystyle \tau }$) и т(${\displaystyle \tau }$), где связь между x и t прямо не указана. Вместо этого x и t определяются параметром ${\displaystyle \tau }$, который является просто параметром системы, возможно, не имеющим самостоятельного объективного значения.

Система была бы описана положением маятника от центра, обозначенным ${\displaystyle x}$, и показания на часах, обозначенные ${\displaystyle t}$. Мы ставим эти переменные в один ряд, вводя фиктивный параметр ${\displaystyle \tau }$,

${\displaystyle x(\tau ),\;\;\;\;t(\tau )}$

чья "эволюция" относительно ${\displaystyle \tau }$ постоянно проводит нас через все возможные корреляции между смещением и показаниями на часах. Очевидно, переменная ${\displaystyle \tau }$ можно заменить любым монотонная функция, ${\displaystyle \tau '=f(\tau )}$. Это то, что делает систему инвариантной к репараметризации. Обратите внимание, что благодаря этой инвариантности к репараметризации теория не может предсказать значение ${\displaystyle x(\tau )}$ или же ${\displaystyle t(\tau )}$ для данного значения ${\displaystyle \tau }$ а только соотношение между этими величинами. Таким образом, динамика определяется этим соотношением.

Динамика этой репараметризационно-инвариантной системы

В действие для параметризованного гармонического осциллятора тогда

${\displaystyle S=\int d\tau {\Big [}{dx \over d\tau }p+{dt \over d\tau }p_{t}-\lambda {\Big (}p_{t}+{p^{2} \over 2m}+{1 \over 2}m\omega ^{2}x^{2}{\Big )}{\Big ]}.}$

куда ${\displaystyle x}$ и ${\displaystyle t}$ канонические координаты и ${\displaystyle p}$ и ${\displaystyle p_{t}}$ являются их сопряженными импульсами соответственно и представляют наше расширенное фазовое пространство (мы покажем, что мы можем восстановить обычные уравнения Ньютона из этого выражения). Написание действия как

${\displaystyle S=\int d\tau {\Big [}{dx \over d\tau }p+{dt \over d\tau }p_{t}-{\mathcal {H}}(x,t;p,p_{t}){\Big ]}}$

мы определяем ${\displaystyle {\mathcal {H}}}$ в качестве

${\displaystyle {\mathcal {H}}(x,t,\lambda ;p,p_{t})=\lambda {\Big (}p_{t}+{p^{2} \over 2m}+{1 \over 2}m\omega ^{2}x^{2}{\Big )}.}$

Уравнения Гамильтона для ${\displaystyle \lambda }$ находятся

${\displaystyle {\partial {\mathcal {H}} \over \partial \lambda }=0}$

что дает ограничение,

${\displaystyle C=p_{t}+{p^{2} \over 2m}+{1 \over 2}m\omega ^{2}x^{2}=0.}$

${\displaystyle C}$ это наше гамильтоново ограничение! Его также можно получить из уравнения движения Эйлера – Лагранжа, учитывая, что действие зависит от ${\displaystyle \lambda }$ но не его ${\displaystyle \tau }$ производная. Тогда переменные расширенного фазового пространства ${\displaystyle x}$, ${\displaystyle t}$, ${\displaystyle p}$, и ${\displaystyle p_{t}}$ вынуждены принимать значения на этой гиперповерхности ограничений расширенного фазового пространства. Мы ссылаемся на ${\displaystyle \lambda C}$ как "размазанная" гамильтонова связь, где ${\displaystyle \lambda }$ - произвольное число. "Размытые" гамильтоновы ограничения говорят нам, как переменная расширенного фазового пространства (или ее функция) эволюционирует относительно ${\displaystyle \tau }$:

${\displaystyle {dx \over d\tau }=\{x,\lambda C\},\;\;\;\;{dp \over d\tau }=\{p,\lambda C\}\;\;\;\;\;\;{dt \over d\tau }=\{t,\lambda C\},\;\;\;\;{dp_{t} \over d\tau }=\{p_{t},\lambda C\}}$

(на самом деле это другие уравнения Гамильтона). Эти уравнения описывают поток или орбиту в фазовом пространстве. В общем имеем

${\displaystyle {dF(x,p,t,p_{t}) \over d\tau }=\{F(x,p,t,p_{t}),\lambda C\}}$

для любой функции фазового пространства ${\displaystyle F}$. Поскольку гамильтонова связь Пуассона коммутирует сама с собой, она сохраняет себя и, следовательно, связь-гиперповерхность. Возможные корреляции между измеряемыми величинами, такими как ${\displaystyle x(\tau )}$ и ${\displaystyle t(\tau )}$ затем соответствуют "орбитам", порожденным ограничением в пределах поверхности ограничения, каждая конкретная орбита отличается друг от друга, скажем, также измеряя значение, скажем, ${\displaystyle p(\tau )}$ вместе с ${\displaystyle x(\tau )}$ и ${\displaystyle t(\tau )}$ за один ${\displaystyle \tau }$-мгновенное; после определения конкретной орбиты для каждого измерения ${\displaystyle t(\tau )}$ мы можем предсказать ценность ${\displaystyle x(\tau )}$ возьму.

Депараметризация

Остальные уравнения Гамильтонова механика находятся

${\displaystyle {dx \over d\tau }={\partial {\mathcal {H}} \over \partial p},\;\;\;\;{dp \over d\tau }=-{\partial {\mathcal {H}} \over \partial x};\;\;\;\;\;\;{dt \over d\tau }={\partial {\mathcal {H}} \over \partial p_{t}},\;\;\;\;{dp_{t} \over d\tau }={\partial {\mathcal {H}} \over \partial t}.}$

При замене нашего действия они дают,

${\displaystyle {dx \over d\tau }=\lambda {p \over m},\;\;\;\;{dp \over d\tau }=-\lambda m\omega ^{2}x;\;\;\;\;\;\;{dt \over d\tau }=\lambda ,\;\;\;\;{dp_{t} \over d\tau }=0,}$

Они представляют собой фундаментальные уравнения, управляющие нашей системой.

В случае параметризованной системы часов и маятника мы, конечно, можем восстановить обычные уравнения движения, в которых ${\displaystyle t}$ независимая переменная:

Сейчас же ${\displaystyle dx/dt}$ и ${\displaystyle dp/dt}$ можно вывести

${\displaystyle {dx \over dt}={dx \over d\tau }{\Big /}{dt \over d\tau }={\lambda p/m \over \lambda }={p \over m}}$

${\displaystyle {dp \over dt}={dp \over d\tau }{\Big /}{dt \over d\tau }={-\lambda m\omega ^{2}x \over \lambda }=-m\omega ^{2}x.}$

Мы восстанавливаем обычное дифференциальное уравнение для простого гармонического осциллятора:

${\displaystyle {d^{2}x \over dt^{2}}=-\omega ^{2}x.}$

У нас также есть ${\displaystyle dp_{t}/dt=dp_{t}/d\tau {\big /}dt/d\tau =0}$ или же ${\displaystyle p_{t}=Const.}$

Тогда нашу гамильтонову связь легко увидеть как условие постоянства энергии! Депараметризация и идентификация временной переменной, относительно которой все развивается, - это процесс, противоположный параметризации. В общем, оказывается, что не все репараметрично-инвариантные системы можно депараметризовать. Общая теория относительности является ярким физическим примером (здесь координаты пространства-времени соответствуют нефизическим ${\displaystyle \tau }$ а гамильтониан - это линейная комбинация ограничений, которые порождают пространственные и временные диффеоморфизмы).

Причина, по которой мы могли депараметризовать здесь

Подчеркивающая причина, по которой мы могли депараметризовать (помимо того факта, что мы уже знаем, что это была в первую очередь искусственная репараметризация), - это математическая форма ограничения, а именно:

${\displaystyle C=p_{t}+C'(x,p)}$.

Подставляя гамильтонову связь в исходное действие, получаем

${\displaystyle S=\int d\tau {\Big [}{dx \over d\tau }p+{dt \over d\tau }p_{t}-\lambda (p_{t}+C'(x,p)){\Big ]}}$

${\displaystyle =\int d\tau {\Big [}{dx \over d\tau }p-{dt \over d\tau }C'(x,p){\Big ]}}$

${\displaystyle =\int dt{\Big [}{dx \over dt}p-{p^{2} \over 2m}+{1 \over 2}m\omega ^{2}x^{2}{\Big ]}}$

что является стандартным действием для гармонического осциллятора. Общая теория относительности является примером физической теории, в которой гамильтонова связь не имеет приведенной выше математической формы в целом и поэтому не может быть депараметризована в целом.

Гамильтониан классической общей теории относительности

в Состав ADM из общая теория относительности пространство-время разбивается на пространственные срезы и время, в качестве основных переменных принимаются индуцированная метрика, ${\displaystyle q_{ab}(x)}$, на пространственном срезе ( метрика индуцированный на пространственном срезе метрикой пространства-времени), и его сопряженная переменная импульса, связанная с внешней кривизной, ${\displaystyle K^{ab}(x)}$, (это говорит нам, как пространственный срез изгибается относительно пространства-времени, и является мерой того, как индуцированная метрика развивается во времени).^[1] Это метрика канонические координаты.

Динамика, такая как временная эволюция полей, контролируется Гамильтонова связь.

Идентичность гамильтоновой связи - главный открытый вопрос в квантовая гравитация, как и извлечение физических наблюдаемые от любого такого конкретного ограничения.

В 1986 г. Абхай Аштекар представил новый набор канонических переменных, Переменные Аштекара представить необычный способ переписать метрические канонические переменные на трехмерных пространственных срезах в терминах SU (2) калибровочное поле и его дополнительная переменная.^[2] В этой переформулировке гамильтониан был значительно упрощен. Это привело к петлевому представлению квантовой общей теории относительности.^[3] и, в свою очередь петля квантовой гравитации.

В рамках петля квантовой гравитации представление Тиман сформулировал математически строгую оператор как предложение как такое ограничение.^[4] Хотя этот оператор определяет полную и непротиворечивую квантовую теорию, возникают сомнения в физической реальности этой теории из-за несоответствия с классической общая теория относительности (квантовая алгебра ограничений замыкается, но она не изоморфна классической алгебре ограничений GR, которая рассматривается как косвенное свидетельство несогласованности, но определенно не доказательство несогласованности), поэтому были предложены варианты.

Метрическая формулировка

Идея заключалась в том, чтобы квантовать канонические переменные ${\displaystyle q_{ab}}$ и ${\displaystyle \pi ^{ab}={\sqrt {q}}(K^{ab}-q^{ab}K_{c}^{c})}$, превращая их в операторы, действующие на волновые функции в пространстве 3-метрик, а затем квантовать гамильтониан (и другие ограничения). Однако вскоре эта программа стала считаться чрезвычайно сложной по разным причинам, одна из которых заключалась в неполиномиальном характере гамильтоновой связи:

${\displaystyle H={\sqrt {det(q)}}(K_{ab}K^{ab}-(K_{a}^{a})^{2}-\;^{3}R)}$

куда ${\displaystyle \;^{3}R}$ скалярная кривизна трех метрики ${\displaystyle q_{ab}(x)}$. Будучи неполиномиальным выражением от канонических переменных и их производных, очень трудно перейти к квантовый оператор.

Выражение с использованием переменных Аштекара

Переменные конфигурации Переменные Аштекара вести себя как ${\displaystyle SU(2)}$ измерительное поле или соединение ${\displaystyle A_{a}^{i}}$. Его канонически сопряженный импульс равен ${\displaystyle {\tilde {E}}_{i}^{a}}$ это уплотненное "электрическое" поле или триада (уплотненная как ${\displaystyle {\tilde {E}}_{i}^{a}={\sqrt {det(q)}}E_{i}^{a}}$). Какое отношение эти переменные имеют к гравитации? Уплотненные триады могут быть использованы для восстановления пространственной метрики через

${\displaystyle det(q)q^{ab}={\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}\delta ^{ij}}$.

Уплотненные триады не уникальны, и фактически можно выполнить локальное в пространстве вращение по внутренним показателям ${\displaystyle i}$. На самом деле это происхождение ${\displaystyle SU(2)}$ калибровочная инвариантность. Это соединение можно использовать для восстановления внешней кривизны. Отношение задается

${\displaystyle A_{a}^{i}=\Gamma _{a}^{i}-iK_{a}^{i}}$

куда ${\displaystyle \Gamma _{a}^{i}}$ относится к спин-соединение, ${\displaystyle \Gamma _{a\;\;i}^{\;\;j}}$, к ${\displaystyle \Gamma _{a}^{i}=\Gamma _{ajk}\epsilon ^{jki}}$ и ${\displaystyle K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}}$.

С точки зрения Переменные Аштекара классическое выражение ограничения дается формулой

${\displaystyle H={\epsilon _{ijk}F_{ab}^{k}{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b} \over {\sqrt {det(q)}}}}$.

куда ${\displaystyle F_{ab}^{k}}$ тензор напряженности поля калибровочного поля ${\displaystyle A_{a}^{i}}$ . Из-за фактора ${\displaystyle 1/{\sqrt {det(q)}}}$ это неполиномиально от переменных Аштекара. Поскольку мы накладываем условие

${\displaystyle H=0}$,

мы могли бы вместо этого рассматривать уплотненный гамильтониан,

${\displaystyle {\tilde {H}}={\sqrt {det(q)}}H=\epsilon _{ijk}F_{ab}^{k}{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}=0}$.

Этот гамильтониан теперь полиномиален от переменных Аштекара. Это событие породило новые надежды на каноническую программу квантовой гравитации.^[5] Хотя переменные Аштекара обладали достоинством упрощения гамильтониана, проблема заключалась в том, что переменные становились сложными. Когда кто-то квантует теорию, это трудная задача - восстановить реальную общую теорию относительности в отличие от сложной общей теории относительности. Также возникли серьезные трудности с преобразованием уплотненного гамильтониана в квантовый оператор.

Один из способов решения проблемы реальных условий заключался в том, чтобы отметить, что если мы примем подпись ${\displaystyle (+,+,+,+)}$, то есть евклидова вместо лоренцевой, то можно сохранить простую форму гамильтониана для вещественных переменных. Затем можно определить то, что называется обобщенным Вращение фитиля восстановить лоренцеву теорию.^[6] Обобщенно, поскольку это преобразование Вика в фазовом пространстве и не имеет ничего общего с аналитическим продолжением параметра времени. ${\displaystyle t}$.

Выражение для реальной формулировки переменных Аштекара

Томас Тиманн обратился к обеим вышеупомянутым проблемам.^[4] Он использовал настоящую связь

${\displaystyle A_{a}^{i}=\Gamma _{a}^{i}+\beta K_{a}^{i}}$

В реальных переменных Аштекара полный гамильтониан имеет вид

${\displaystyle H=-\zeta {\epsilon _{ijk}F_{ab}^{k}{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b} \over {\sqrt {det(q)}}}+2{\zeta \beta ^{2}-1 \over \beta ^{2}}{({\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}-{\tilde {E}}_{j}^{a}{\tilde {E}}_{i}^{b}) \over {\sqrt {det(q)}}}(A_{a}^{i}-\Gamma _{a}^{i})(A_{b}^{j}-\Gamma _{b}^{j})=H_{E}+H'}$.

где постоянная ${\displaystyle \beta }$ Барберо-Параметр Иммирзи.^[7] Постоянная ${\displaystyle \zeta }$ равно -1 для лоренцевой подписи и +1 для евклидовой подписи. В ${\displaystyle \Gamma _{a}^{i}}$ имеют сложные отношения с уплотненными триадами и вызывают серьезные проблемы при квантовании. Переменные Аштекара можно рассматривать как выбор ${\displaystyle \beta =i}$ чтобы второй, более сложный член был обращен в нуль (первый член обозначается ${\displaystyle H_{E}}$ потому что для евклидовой теории этот термин остается для реального выбора ${\displaystyle \beta =\pm 1}$). Также у нас все еще есть проблема ${\displaystyle 1/{\sqrt {det(q)}}}$ фактор.

Тиманн смог заставить это работать по-настоящему ${\displaystyle \beta }$. Сначала он мог упростить неприятный ${\displaystyle 1/{\sqrt {det(q)}}}$ используя личность

${\displaystyle \{A_{c}^{k},V\}={\epsilon _{abc}\epsilon ^{ijk}{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b} \over {\sqrt {det(q)}}}}$

куда ${\displaystyle V}$ объем,

${\displaystyle V=\int d^{3}x{\sqrt {det(q)}}={1 \over 6}\int d^{3}x{\sqrt {|{\tilde {E}}_{i}^{a}{\tilde {E}}_{j}^{b}{\tilde {E}}_{k}^{c}\epsilon ^{ijk}\epsilon _{abc}|}}}$.

Первый член гамильтоновой связи принимает вид

${\displaystyle H_{E}=\{A_{c}^{k},V\}F_{ab}^{k}{\tilde {\epsilon }}^{abc}}$

при использовании личности Тимана. Эта скобка Пуассона заменяется коммутатором при квантовании. Оказывается, аналогичный прием можно использовать и для второго члена. Почему ${\displaystyle \Gamma _{a}^{i}}$ дается уплотненными триадами ${\displaystyle {\tilde {E}}_{i}^{a}}$? На самом деле это происходит из закона Гаусса.

${\displaystyle D_{a}{\tilde {E}}_{i}^{a}=0}$.

Мы можем решить эту проблему так же, как Леви-Чивита соединение можно рассчитать по формуле ${\displaystyle \nabla _{c}g_{ab}=0}$; вращая различные индексы, а затем складывая и вычитая их. Результат сложный и нелинейный. Чтобы обойти проблемы, связанные с этим сложным соотношением, Тиман сначала определяет калибровочно-инвариантную величину Гаусса

${\displaystyle K=\int d^{3}xK_{a}^{i}{\tilde {E}}_{i}^{a}}$

куда ${\displaystyle K_{a}^{i}=K_{ab}{\tilde {E}}^{ai}/{\sqrt {det(q)}}}$, и отмечает, что

${\displaystyle K_{a}^{i}=\{A_{a}^{i},K\}}$.

Затем мы можем написать

${\displaystyle A_{a}^{i}-\Gamma _{a}^{i}=\beta K_{a}^{i}=\beta \{A_{a}^{i},K\}}$

и как таковой найти выражение в терминах переменной конфигурации ${\displaystyle A_{a}^{i}}$ и ${\displaystyle K}$. Для второго члена гамильтониана получаем

${\displaystyle H'=\epsilon ^{abc}\epsilon _{ijk}\{A_{a}^{i},K\}\{A_{b}^{j},K\}\{A_{c}^{k},V\}}$.

Почему квантовать проще ${\displaystyle K}$? Это потому, что его можно переписать в единицах величин, которые мы уже знаем, как квантовать. Конкретно ${\displaystyle K}$ можно переписать как

${\displaystyle K=-\{V,\int d^{3}xH_{E}\}}$

где мы использовали, что интегрированный уплотненный след внешней кривизны является «производной по времени от объема».

Рекомендации

1. Гравитация Чарльз В. Миснер, Кип С. Торн, Джон Арчибальд Уиллер, опубликовано В. Х. Фриманом и компанией. Нью-Йорк.
2. Аштекар, Абхай (1986-11-03). «Новые переменные для классической и квантовой гравитации». Письма с физическими проверками. Американское физическое общество (APS). 57 (18): 2244–2247. Дои:10.1103 / Physrevlett.57.2244. ISSN  0031-9007.
3. Ровелли, Карло; Смолин, Ли (1988-09-05). «Теория узлов и квантовая гравитация». Письма с физическими проверками. Американское физическое общество (APS). 61 (10): 1155–1158. Дои:10.1103 / Physrevlett.61.1155. ISSN  0031-9007.
4. Тиманн, Т. (1996). «Формулировка без аномалий непертурбативной четырехмерной лоренцевой квантовой гравитации». Письма по физике B. Elsevier BV. 380 (3–4): 257–264. arXiv:gr-qc / 9606088. Дои:10.1016/0370-2693(96)00532-1. ISSN  0370-2693.
5. Посмотреть книгу Лекции о непертурбативной канонической гравитации для получения более подробной информации об этом и последующих разработках. Впервые опубликовано в 1991 году. World Scientific Publishing Co. Pte. LtD.
6. Тиманн, Т. (1996-06-01). «Условия реальности, вызывающие преобразования для квантовой калибровочной теории поля и квантовой гравитации». Классическая и квантовая гравитация. IOP Publishing. 13 (6): 1383–1403. arXiv:gr-qc / 9511057. Дои:10.1088/0264-9381/13/6/012. ISSN  0264-9381.
7. Барберо Г., Дж. Фернандо (1995-05-15). «Реальные аштекарские переменные для лоренцевой сигнатуры пространства-времени». Физический обзор D. Американское физическое общество (APS). 51 (10): 5507–5510. arXiv:gr-qc / 9410014. Дои:10.1103 / Physrevd.51.5507. ISSN  0556-2821.

внешняя ссылка

• Обзор Карло Ровелли
• Статья Тимана в Physics Letters
• Хорошая информация о LQG