Гиперпрямоугольник - Hyperrectangle

Гиперпрямоугольник п-ортоп
Прямоугольный кубовид это 3-ортотоп
Тип	Призма
Грани	2п
Вершины	2^п
Символ Шлефли	{} × {} ... × {}^[1]
Диаграмма Кокстера-Дынкина	...
Группа симметрии	[2^п−1], порядок 2^п
Двойной	Прямоугольный п-фузея
Характеристики	выпуклый, зоноэдр, изогональный

В геометрия, п-ортоп^[2] (также называемый гипер прямоугольник или коробка) является обобщением прямоугольник для более высоких измерений, формально определяемый как Декартово произведение из интервалы.

Типы

Трехмерный ортотоп также называется правильным прямоугольником призма, прямоугольная кубовид, или прямоугольный параллелепипед.

Частный случай н-ортотоп, где все ребра равной длины, - н-куб.^[2]

По аналогии, термин «гипер прямоугольник» или «прямоугольник» относится к декартовым произведениям ортогональный интервалы других типов, например диапазоны клавиш в теория баз данных или диапазоны целые числа, скорее, чем действительные числа.^[3]

Двойной многогранник

п-фузея
Пример: 3-фузил
Грани	2п
Вершины	2^п
Символ Шлефли	{} + {} + ... + {}
Диаграмма Кокстера-Дынкина	...
Группа симметрии	[2^п−1], порядок 2^п
Двойной	п-ортоп
Характеристики	выпуклый, изотопный

В двойственный многогранник из п-ортоп по-разному называли прямоугольным n-ортоплекс, ромбический п-фусил, или п-лепешка. Он построен 2п точки, расположенные в центре прямоугольных граней ортотопов.

An п-фусила Символ Шлефли можно представить в виде суммы п ортогональные отрезки: {} + {} + ... + {}.

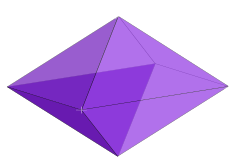
1-фузил - это отрезок. 2-фузил - это ромб. Его плоские сечения во всех парах осей равны ромбовидные.

п	Пример изображения
1	{ }
2	{ } + { }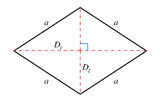
3	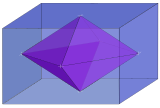Ромбический 3-ортоплекс внутри 3-ортотоп { } + { } + { }

Смотрите также

Примечания

^ N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, 11.5 Сферические группы Кокстера, стр.251
^ ^а ^б Кокстер, 1973
^ См. Например Чжан, И; Мунагала, Камеш; Ян, июнь (2011), «Хранение матриц на диске: пересмотр теории и практики» (PDF), Proc. VLDB, 4 (11): 1075–1086.

внешняя ссылка

[1] N.W. Джонсон: Геометрии и преобразования, (2018) ISBN 978-1-107-10340-5 Глава 11: Конечные группы симметрии, 11.5 Сферические группы Кокстера, стр.251

[regpoly-2] а ^б Кокстер, 1973

[3] См. Например Чжан, И; Мунагала, Камеш; Ян, июнь (2011), «Хранение матриц на диске: пересмотр теории и практики» (PDF), Proc. VLDB, 4 (11): 1075–1086.

[1]

[2]

[3]

Измерение
Размерные пространства	Векторное пространство Евклидово пространство Аффинное пространство Проективное пространство Бесплатный модуль Многообразие Алгебраическое многообразие Пространство-время
Другие размеры	Krull Покрытие Лебега Индуктивный Хаусдорф Минковский Фрактал Степени свободы
Многогранники и формы	Гиперплоскость Гиперповерхность Гиперкуб Гиперсфера Гиперпрямоугольник Демигиперкуб Кросс-многогранник Симплекс
Размеры по номеру	Нуль Один Два Три Четыре Пять Шесть Семь 8 9 п-размеры Отрицательные размеры
Категория