Подключение (векторный набор) - Connection (vector bundle)

Эта статья о связях на векторных расслоениях. О других типах связей в математике см. связь (математика).

В математика, и особенно дифференциальная геометрия и калибровочная теория, а связь на пучок волокон это устройство, которое определяет понятие параллельный транспорт на пачке; то есть способ «соединить» или идентифицировать волокна в близлежащих точках. Чаще всего случается, что линейное соединение на векторный набор, для чего понятие параллельного транспорта должно быть линейный. Линейная связь эквивалентно определяется ковариантная производная, оператор, дифференцирующий разделы пучка вдоль касательные направления в базовом многообразии таким образом, чтобы параллельные участки имели нулевую производную. Линейные связности обобщают на произвольные векторные расслоения Леви-Чивита связь на касательный пучок из Риманово многообразие, который дает стандартный способ дифференцировать векторные поля. Нелинейные связи обобщить это понятие на расслоения, слои которых не обязательно линейны.

Линейные связи также называют Кошульские связи после Жан-Луи Кошул, который дал алгебраический каркас для их описания (Кошул 1950 ).

В этой статье связь на векторном пучке определяется с использованием общепринятого математического обозначения, в котором координаты не выделяются. Однако регулярно используются и другие обозначения: в общая теория относительности, вычисления векторных расслоений обычно записываются с использованием индексированных тензоров; в калибровочная теория подчеркиваются эндоморфизмы слоев векторного пространства. Различные обозначения эквивалентны, как описано в статье о метрические соединения (сделанные там комментарии относятся ко всем векторным расслоениям).

Мотивация

Сечение векторного расслоения обобщает понятие функции на многообразии в том смысле, что стандартная вектор-функция ${\displaystyle f:M\to \mathbb {R} ^{n}}$ можно рассматривать как часть тривиального векторного расслоения ${\displaystyle M\times \mathbb {R} ^{n}\to M}$. Поэтому естественно спросить, можно ли дифференцировать сечение по аналогии с тем, как дифференцировать векторное поле. Когда векторное расслоение касательный пучок к Риманово многообразие, на этот вопрос естественно отвечает Леви-Чивита связь которая представляет собой единственную связность без кручения, совместимую с римановой метрикой на касательном расслоении. В общем, такого естественного выбора способа разграничения разделов нет.

Сечение расслоения можно рассматривать как обобщенную функцию от основания к слоям векторного расслоения. Это можно визуализировать с помощью графика раздела, как на рисунке выше.

Модельный случай состоит в том, чтобы дифференцировать ${\displaystyle m}$-компонентное векторное поле ${\displaystyle X:\mathbb {R} ^{n}\to \mathbb {R} ^{m}}$ на евклидовом пространстве ${\displaystyle \mathbb {R} ^{n}}$. В этой настройке производная ${\displaystyle dX}$ в какой-то момент ${\displaystyle x\in \mathbb {R} ^{n}}$ в направлении ${\displaystyle v\in \mathbb {R} ^{n}}$ можно просто определить как

${\displaystyle dX(v)(x)=\lim _{t\to 0}{\frac {X(x+tv)-X(x)}{t}}.}$

Обратите внимание, что для каждого ${\displaystyle x\in \mathbb {R} ^{n}}$, мы определили новый вектор ${\displaystyle dX(v)(x)\in \mathbb {R} ^{m}}$ так что производная от ${\displaystyle X}$ в направлении ${\displaystyle v}$ дала новый ${\displaystyle m}$-компонентное векторное поле на ${\displaystyle \mathbb {R} ^{n}}$.

При переходе в раздел ${\displaystyle X\in \Gamma (E)}$ векторного расслоения ${\displaystyle E}$ на коллекторе ${\displaystyle M}$, с этим определением возникают две ключевые проблемы. Во-первых, поскольку многообразие не имеет линейной структуры, член ${\displaystyle x+tv}$ не имеет смысла на ${\displaystyle M}$. Вместо этого человек выбирает путь ${\displaystyle \gamma :(-1,1)\to M}$ такой, что ${\displaystyle \gamma (0)=x,\gamma '(0)=v}$ и вычисляет

${\displaystyle dX(v)(x)=\lim _{t\to 0}{\frac {X(\gamma (t))-X(\gamma (0))}{t}}.}$

Однако это все еще не имеет смысла, потому что ${\displaystyle X(\gamma (t))\in E_{\gamma (t)}}$ вектор в слое над ${\displaystyle \gamma (t)}$, и ${\displaystyle X(\gamma (0))=X(x)\in E_{x}}$, волокно над ${\displaystyle x}$, которое представляет собой другое векторное пространство. Это означает, что нет никакого смысла в вычитании этих двух членов, лежащих в разных векторных пространствах.

Цель состоит в том, чтобы решить вышеупомянутую загадку, придумав способ дифференцировать разделы векторного расслоения в направлении векторных полей и получить обратно еще один фрагмент векторного расслоения. Есть три возможных решения этой проблемы. Все три требуют создания выбор о том, как различать сечения, и только в особых случаях, таких как касательное расслоение на римановом многообразии, есть естественный такой выбор.

1. (Параллельный транспорт ) Поскольку проблема в том, что векторы ${\displaystyle X(\gamma (t))}$ и ${\displaystyle X(x)}$ лежат в разных волокнах ${\displaystyle E}$, одним из решений является определение изоморфизма ${\displaystyle P_{t}^{\gamma }:E_{\gamma (t)}\to E_{x}}$ для всех ${\displaystyle t}$ близко к нулю. Используя этот изоморфизм, можно транспортировать ${\displaystyle X(\gamma (t))}$ к волокну ${\displaystyle E_{x}}$ а потом заметьте разницу. Явно

${\displaystyle dX(v)(x)=\lim _{t\to 0}{\frac {P_{t}^{\gamma }X(\gamma (t))-X(\gamma (0))}{t}}.}$

Это параллельный транспорт, а выбор изоморфизмов ${\displaystyle P_{t}^{\gamma }}$ для всех кривых ${\displaystyle \gamma }$ в ${\displaystyle M}$ можно рассматривать как определение того, как различать раздел.

1. (Связь Ehresmann ) Используйте понятие дифференциал карты гладких многообразий. Секция ${\displaystyle s\in \Gamma (E)}$ по определению гладкое отображение ${\displaystyle s:M\to E}$ такой, что ${\displaystyle \pi \circ s=\operatorname {Id} }$. Это имеет дифференциал ${\displaystyle ds:TM\to TE}$, со свойством, что ${\displaystyle ds(X)\in \Gamma (TE)}$ для векторного поля ${\displaystyle X\in \Gamma (TM)}$. Однако вместо этого хотелось бы ${\displaystyle ds(X)}$ быть частью ${\displaystyle E}$ сам. Фактически, вертикальный пучок ${\displaystyle V\subset TE}$ это откат ${\displaystyle E}$ вместе ${\displaystyle E}$ с тем же волокном, что и ${\displaystyle E\to M}$. Если выбрать проекцию ${\displaystyle \nu :TE\to V}$ векторных пучков, при компоновке с этой проекцией ${\displaystyle ds(X)}$ обратно в ${\displaystyle E}$. Это называется линейным Связь Ehresmann на векторном расслоении ${\displaystyle E\to M}$. Есть много вариантов операторов проекции ${\displaystyle \nu :TE\to V}$ так что в общем есть много разных способов дифференцировать векторное поле.

1. (Ковариантная производная Третье решение - абстрагироваться от свойств, которыми должна обладать производная части векторного расслоения, и принимать это как аксиоматическое определение. Это понятие связь или ковариантная производная описано в этой статье. Можно показать, что оба других двух вышеприведенных подхода эквивалентны этому аксиоматическому определению дифференцирования.

Формальное определение

Позволять E → M быть гладким векторный набор через дифференцируемое многообразие M. Обозначим пространство гладких разделы из E через Γ (E). А связь на E это ℝ-линейная карта

${\displaystyle \nabla :\Gamma (E)\to \Gamma (T^{*}M\otimes E)}$

так что Правило Лейбница

${\displaystyle \nabla (f\sigma )=f\nabla \sigma +df\otimes \sigma }$

относится ко всем гладкие функции ж на M и все гладкие сечения σ E.

Если Икс является касательным векторным полем на M (т.е. часть касательный пучок TM) можно определить ковариантная производная по Икс

${\displaystyle \nabla _{X}:\Gamma (E)\to \Gamma (E)}$

по контракту Икс с полученным ковариантным индексом в связи: ∇_Икс σ = (∇σ) (Икс). Ковариантная производная удовлетворяет:

${\displaystyle {\begin{aligned}&\nabla \!_{X}(\sigma _{1}{+}\sigma _{2})\ =\ \nabla \!_{X}\sigma _{1}+\nabla \!_{X}\sigma _{2}\\&\nabla \!_{(X_{1}{+}X_{2})}\sigma \ =\ \nabla \!_{X_{1}}\sigma +\nabla \!_{X_{2}}\sigma \\&\nabla \!_{X}(f\sigma )\ =\ f\,\nabla \!_{X}\sigma +X(f)\sigma \\&\nabla \!_{fX}\sigma \ =\ f\,\nabla \!_{X}\sigma .\end{aligned}}}$

И наоборот, любой оператор, удовлетворяющий указанным выше свойствам, определяет соединение на E и соединение в этом смысле также известно как ковариантная производная на E.

Индуцированные соединения

Учитывая векторное расслоение ${\displaystyle E\to M}$, есть много связанных пакетов ${\displaystyle E}$ которые можно построить, например двойственное векторное расслоение ${\displaystyle E^{*}}$, тензорные степени ${\displaystyle E^{\otimes k}}$, симметричные и антисимметричные тензорные степени ${\displaystyle S^{k}E,\Lambda ^{k}E}$, а прямые суммы ${\displaystyle E^{\oplus k}}$. Связь на ${\displaystyle E}$ индуцирует связь на любом из этих ассоциированных пучков. Простота перехода между соединениями в связанных связках более элегантно описывается теорией основные связки, но здесь мы представляем некоторые из основных индуцированных связей.

Данный ${\displaystyle \nabla }$ связь на ${\displaystyle E}$индуцированная двойное соединение ${\displaystyle \nabla ^{*}}$ на ${\displaystyle E^{*}}$ определяется

${\displaystyle d(\langle \xi ,s\rangle )(X)=\langle \nabla _{X}^{*}\xi ,s\rangle +\langle \xi ,\nabla _{X}s\rangle .}$

Здесь ${\displaystyle X\in \Gamma (TM)}$ гладкое векторное поле, ${\displaystyle s\in \Gamma (E)}$ это раздел ${\displaystyle E}$, и ${\displaystyle \xi \in \Gamma (E^{*})}$ секция двойного пучка, и ${\displaystyle \langle \cdot ,\cdot \rangle }$ естественное спаривание между векторным пространством и его двойником (возникающее на каждом слое между ${\displaystyle E}$ и ${\displaystyle E^{*}}$). Обратите внимание, что это определение, по сути, требует, чтобы ${\displaystyle \nabla ^{*}}$ быть связью на ${\displaystyle E^{*}}$ так что естественный правило продукта удовлетворен для сопряжения ${\displaystyle \langle \cdot ,\cdot \rangle }$.

Данный ${\displaystyle \nabla ^{E},\nabla ^{F}}$ связи на двух векторных расслоениях ${\displaystyle E,F\to M}$определить соединение тензорного произведения по формуле

${\displaystyle (\nabla ^{E}\otimes \nabla ^{F})_{X}(s\otimes t)=\nabla _{X}^{E}(s)\otimes t+s\otimes \nabla _{X}^{F}(t).}$

Здесь у нас есть ${\displaystyle s\in \Gamma (E),t\in \Gamma (F),X\in \Gamma (TM)}$. Обратите внимание, это естественный способ комбинирования ${\displaystyle \nabla ^{E},\nabla ^{F}}$ для обеспечения соблюдения правила произведения для соединения тензорного произведения. Аналогичным образом определим прямая связь от

${\displaystyle (\nabla ^{E}\oplus \nabla ^{F})_{X}(s\oplus t)=\nabla _{X}^{E}(s)\oplus \nabla _{X}^{F}(t),}$

где ${\displaystyle s\oplus t\in \Gamma (E\oplus F)}$.

Поскольку внешнюю степень и симметричную мощность векторного расслоения можно рассматривать как подпространства тензорной степени, ${\displaystyle S^{k}E,\Lambda ^{k}E\subset E^{\otimes k}}$, определение связи тензорного произведения прямо применяется к этому параметру. А именно, если ${\displaystyle \nabla }$ это связь на ${\displaystyle E}$, у одного есть тензорное силовое соединение путем повторных применений на указанном выше соединении тензорного произведения. У нас также есть симметричное соединение продукта определяется

${\displaystyle \nabla _{X}^{\odot 2}(s\cdot t)=\nabla _{X}s\cdot t+s\cdot \nabla _{X}t}$

и подключение внешнего продукта определяется

${\displaystyle \nabla _{X}^{\wedge 2}(s\wedge t)=\nabla _{X}s\wedge t+s\wedge \nabla _{X}t}$

для всех ${\displaystyle s,t\in \Gamma (E),X\in \Gamma (TM)}$. Повторное применение этих продуктов дает наведенное симметричное питание и внешние силовые подключения ${\displaystyle S^{k}E}$ и ${\displaystyle \Lambda ^{k}E}$ соответственно.

В итоге получаем индуцированную связь ${\displaystyle \nabla ^{\operatorname {End} {E}}}$ на векторном расслоении ${\displaystyle \operatorname {End} (E)=E^{*}\otimes E}$, то связь эндоморфизма. Это просто тензорное произведение двойственной связи ${\displaystyle \nabla ^{*}}$ на ${\displaystyle E^{*}}$ и ${\displaystyle \nabla }$ на ${\displaystyle E}$. Если ${\displaystyle s\in \Gamma (E)}$ и ${\displaystyle u\in \Gamma (\operatorname {End} (E))}$, так что композиция ${\displaystyle u(s)\in \Gamma (E)}$ кроме того, тогда выполняется следующее правило произведения:

${\displaystyle \nabla _{X}(u(s))=\nabla _{X}^{\operatorname {End} (E)}(u)(s)+u(\nabla _{X}(s)).}$

Внешние ковариантные производные и векторнозначные формы

Смотрите также: Внешняя ковариантная производная

Позволять E → M - векторное расслоение. An E-значная дифференциальная форма степени р это раздел тензорное произведение пучок:

${\displaystyle E\otimes \bigwedge ^{r}T^{*}M.}$

Пространство таких форм обозначим через

${\displaystyle \Omega ^{r}(E)=\Omega ^{r}(M;E)=\Gamma \left(E\otimes \bigwedge ^{r}T^{*}M\right).}$

An E-значная 0-форма - это всего лишь часть пакета E. Это,

${\displaystyle \Omega ^{0}(E)=\Gamma (E).}$

В этих обозначениях связь по E → M линейная карта

${\displaystyle \nabla :\Omega ^{0}(E)\to \Omega ^{1}(E).}$

Тогда связь можно рассматривать как обобщение внешняя производная к векторным расслоенным значным формам. Фактически, учитывая связь ∇ на E существует единственный способ продолжить ∇ до внешняя ковариантная производная

${\displaystyle d^{\nabla }:\Omega ^{r}(E)\to \Omega ^{r+1}(E).}$

В отличие от обычной внешней производной, обычно (d^∇)² ≠ 0. На самом деле (d^∇)² напрямую связано с кривизной связности ∇ (см. ниже ).

Аффинные свойства множества связей

Каждое векторное расслоение над многообразием допускает связность, которая может быть доказана с помощью разделы единства. Однако связи не уникальны. Если ∇₁ и ∇₂ две связи на E → M то их разница в C^∞ -линейный оператор. Это,

${\displaystyle (\nabla _{1}-\nabla _{2})(f\sigma )=f(\nabla _{1}\sigma -\nabla _{2}\sigma )}$

для всех гладких функций ж на M и все гладкие сечения σ E. Отсюда следует, что разность ∇₁ − ∇₂ индуцирована одной формой на M со значениями в расслоении эндоморфизмов End (E) = E⊗E*:

${\displaystyle (\nabla _{1}-\nabla _{2})\in \Omega ^{1}(M;\mathrm {End} \,E).}$

Наоборот, если ∇ - связность на E и А является одной формой на M со значениями в End (E), то ∇ +А это связь на E.

Другими словами, пространство связей на E является аффинное пространство для Ω¹(Конец E). Это аффинное пространство обычно обозначается ${\displaystyle {\mathcal {A}}}$.

Связь с принципалом и связями Эресмана

Позволять E → M - векторное расслоение ранга k и пусть F (E) быть главный комплект кадров из E. Потом (основное) подключение на 'F(E) индуцирует связь на E. Сначала обратите внимание, что разделы E находятся во взаимно-однозначной переписке с правоэквивариантный отображает F (E) → р^k. (В этом можно убедиться, рассмотрев откат из E над F (E) → M, который изоморфен тривиальная связка F (E) × р^k.) Для сечения σ множества E пусть соответствующее эквивариантное отображение есть ψ (σ). Ковариантная производная на E тогда дается

${\displaystyle \psi (\nabla _{X}\sigma )=X^{H}(\psi (\sigma ))}$

где Икс^ЧАС это горизонтальный подъем из Икс из M к F (E). (Напомним, что горизонтальный подъем определяется связностью на F (E).)

И наоборот, соединение на E определяет связность на F (E), и эти две конструкции взаимно обратны.

Связь на E также определяется эквивалентным образом линейное соединение Эресмана на E. Это предоставляет один метод для создания связанного основного подключения.

Местное выражение

Позволять E → M - векторное расслоение ранга k, и разреши U быть открытым подмножеством M в течение которого E тривиально. Учитывая местный гладкая рама (е₁, ..., е_k) из E над U, любое сечение σ E можно записать как ${\displaystyle \sigma =\sigma ^{\alpha }e_{\alpha }}$ (Обозначения Эйнштейна предполагается). Связь на E ограниченный U затем принимает форму

${\displaystyle \nabla \sigma =e_{\alpha }\otimes \left(d\sigma ^{\alpha }+\sigma ^{\beta }{\omega ^{\alpha }}_{\beta }\right),}$

что означает, учитывая каждый компонент:

${\displaystyle \left(\nabla \sigma \right)^{\alpha }=d\sigma ^{\alpha }+\sigma ^{\beta }{\omega ^{\alpha }}_{\beta },}$

где

${\displaystyle e_{\alpha }\otimes {\omega ^{\alpha }}_{\beta }=\nabla e_{\beta }.}$

Здесь ${\displaystyle {\omega ^{\alpha }}_{\beta }}$ определяет k × k матрица одноформ на U. Фактически, для любой такой матрицы приведенное выше выражение определяет связь на E ограниченный U. Это потому что ${\displaystyle {\omega ^{\alpha }}_{\beta }}$ определяет одноформу ω со значениями в End (E) и это выражение определяет ∇ как связность d + ω, где d - тривиальная связь на E над U определяется путем различения компонентов секции с помощью локальной рамки. В этом контексте ω иногда называют форма подключения относительно локального репера.

Если U - координатная окрестность с координатами (Икс^я) то мы можем написать

${\displaystyle {\omega ^{\alpha }}_{\beta }={{\omega _{i}}^{\alpha }}_{\beta }\,dx^{i}.}$

Обратите внимание на смесь координатных индексов (я) и индексы слоев (α, β) в этом выражении.

Коэффициентные функции ${\displaystyle {{\omega _{i}}^{\alpha }}_{\beta }}$ тензорны по индексу я (они определяют одноформу), но не по индексам α и β. Закон преобразования для показателей волокна более сложен. Позволять (ж₁, ..., ж_k) - еще один гладкий локальный репер над U и обозначим изменение координатной матрицы т, то есть:

${\displaystyle f_{\alpha }\ =\ e_{\beta }\,{t^{\beta }}_{\alpha }.}$

Матрица связи по отношению к кадру (ж_α) тогда задается матричным выражением

${\displaystyle \varpi =t^{-1}\omega t+t^{-1}dt.}$

Здесь dт - матрица одноформ, полученная взятием внешней производной от компонент т.

Ковариантная производная в локальных координатах и ​​по полю локальной системы отсчета (е_α) дается выражением

${\displaystyle \nabla _{X}\sigma =e_{\alpha }\otimes X^{i}\left(\partial _{i}\sigma ^{\alpha }+{{\omega _{i}}^{\alpha }}_{\beta }\sigma ^{\beta }\right).}$

Например, если мы насытим аргумент индекса the базисным касательным вектором ${\displaystyle \partial _{i}={\frac {\partial }{\partial x^{i}}}}$, и установите ${\displaystyle \nabla _{i}:=\nabla _{\partial _{i}}}$, у нас есть:

${\displaystyle \left(\nabla _{i}\sigma \right)^{\alpha }={\frac {\partial \sigma ^{\alpha }}{\partial x^{i}}}+\sigma ^{\beta }{{\omega _{i}}^{\alpha }}_{\beta }.}$

Параллельный транспорт и голономия

Связность ∇ на векторном расслоении E → M определяет понятие параллельный транспорт на E по кривой в M. Пусть γ: [0, 1] → M быть гладким дорожка в M. Сечение σ из E вдоль γ называется параллельно если

${\displaystyle \nabla _{{\dot {\gamma }}(t)}\sigma =0}$

для всех т ∈ [0, 1]. В равной степени можно рассматривать обратный пакет γ *E из E пользователя γ. Это векторное расслоение над [0, 1] со слоем E_{γ (т)} над т ∈ [0, 1]. Подключение ∇ на E возвращается к связности на γ *E. Сечение σ кривой γ *E параллельна тогда и только тогда, когда γ * ∇ (σ) = 0.

Предположим, что γ - путь из Икс к у в M. Приведенное выше уравнение, определяющее параллельные участки, является уравнением первого порядка обыкновенное дифференциальное уравнение (ср. местное выражение выше) и поэтому имеет уникальное решение для каждого возможного начального условия. То есть для каждого вектора v в E_Икс существует единственное параллельное сечение σ кривой γ *E с σ (0) = v. Определить параллельная транспортная карта

${\displaystyle \tau _{\gamma }:E_{x}\to E_{y}\,}$

по τ_γ(v) = σ (1). Можно показать, что τ_γ это линейный изоморфизм.

Как восстановить ковариантную производную соединения из его параллельного переноса. Ценности ${\displaystyle s(\gamma (t))}$ раздела ${\displaystyle s\in \Gamma (E)}$ параллельно транспортируются по пути ${\displaystyle \gamma }$ вернуться к ${\displaystyle \gamma (0)=x}$, а затем берется ковариантная производная в фиксированном векторном пространстве, слой ${\displaystyle E_{x}}$ над ${\displaystyle x}$.

Параллельный транспорт может использоваться для определения группа голономии связи ∇ в точке Икс в M. Это подгруппа GL (E_Икс), состоящий из всех параллельных транспортных карт из петли основанный на Икс:

${\displaystyle \mathrm {Hol} _{x}=\{\tau _{\gamma }:\gamma {\text{ is a loop based at }}x\}.\,}$

Группа голономии связности тесно связана с кривизной связности (Амвросий Певец 1953 ).

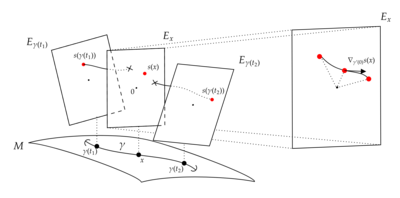
Соединение может быть восстановлено от его параллельных транспортных операторов следующим образом. Если ${\displaystyle X\in \Gamma (TM)}$ - векторное поле и ${\displaystyle s\in \Gamma (E)}$ раздел, в точке ${\displaystyle x\in M}$ выбрать интегральная кривая ${\displaystyle \gamma :(-\varepsilon ,\varepsilon )\to M}$ за ${\displaystyle X}$ в ${\displaystyle x}$. Для каждого ${\displaystyle t\in (-\varepsilon ,\varepsilon )}$ мы напишем ${\displaystyle \tau _{t}:E_{\gamma (t)}\to E_{x}}$ для параллельной транспортной карты, путешествующей по ${\displaystyle \gamma }$ из ${\displaystyle t}$ к ${\displaystyle 0}$. В частности для каждого ${\displaystyle t\in (-\varepsilon ,\varepsilon )}$, у нас есть ${\displaystyle \tau _{t}s(\gamma (t))\in E_{x}}$. потом ${\displaystyle t\mapsto \tau _{t}s(\gamma (t))}$ определяет кривую в векторном пространстве ${\displaystyle E_{x}}$, которые можно дифференцировать. Ковариантная производная восстанавливается как

${\displaystyle \nabla _{X}s(x)={\frac {d}{dt}}\left(\tau _{t}s(\gamma (t))\right)_{t=0}.}$

Это демонстрирует, что эквивалентное определение соединения дается указанием всех параллельных транспортных изоморфизмов ${\displaystyle \tau _{\gamma }}$ между волокнами ${\displaystyle E}$ и взяв это выражение как определение ${\displaystyle \nabla }$.

Кривизна

Смотрите также: Форма кривизны

В кривизна соединения ∇ на E → M это 2-форма F^∇ на M со значениями в расслоении эндоморфизмов End (E) = E⊗E*. Это,

${\displaystyle F^{\nabla }\in \Omega ^{2}(\mathrm {End} \,E)=\Gamma (\mathrm {End} \,E\otimes \Lambda ^{2}T^{*}M).}$

Он определяется выражением

${\displaystyle F^{\nabla }(X,Y)(s)=\nabla _{X}\nabla _{Y}s-\nabla _{Y}\nabla _{X}s-\nabla _{[X,Y]}s}$

где Икс и Y касательные векторные поля на M и s это раздел E. Надо проверить это F^∇ является C^∞ -линейный в обоих Икс и Y и что он на самом деле определяет эндоморфизм расслоения E.

Как уже упоминалось над, ковариантная внешняя производная d^∇ при воздействии на E-значные формы. Оператор (d^∇)² однако строго тензорно (т. е. C^∞-линейный). Это означает, что он индуцирован 2-формой со значениями в End (E). Эта 2-форма в точности соответствует приведенной выше форме кривизны. Для E-значной формы σ имеем

${\displaystyle (d^{\nabla })^{2}\sigma =F^{\nabla }\wedge \sigma .}$

А плоское соединение форма кривизны тождественно равна нулю.

Локальная форма и структурное уравнение Картана

Форма кривизны имеет локальное описание, называемое Структурное уравнение Картана. Если ${\displaystyle \nabla }$ имеет местную форму ${\displaystyle \omega }$ на некотором тривиализирующем открытом подмножестве ${\displaystyle U\subset M}$ за ${\displaystyle E}$, тогда

${\displaystyle F^{\nabla }=d\omega +\omega \wedge \omega }$

на ${\displaystyle U}$. Чтобы уточнить, ${\displaystyle \nabla =d+\omega }$ где ${\displaystyle \omega \in \Omega ^{1}(U,\operatorname {End} (E))}$ - эндоморфизм-значная однозначная форма. Для простоты предположим ${\displaystyle \omega =\alpha \otimes u}$ для одноразовой ${\displaystyle \alpha \in \Omega ^{1}(U)}$ и эндоморфизм ${\displaystyle u\in \Gamma (U,\operatorname {End} (E))}$. Затем мы используем соглашения

${\displaystyle d(\alpha \otimes u)=(d\alpha )\otimes u,\quad (\alpha \otimes u)\wedge (\beta \otimes v)=(\alpha \wedge \beta )\otimes uv,}$

где ${\displaystyle \beta \otimes v}$ - еще одна однозначная форма эндоморфизма. В общем ${\displaystyle \omega }$ будет суммой простых тензоров этого вида, а операторы ${\displaystyle d}$ и ${\displaystyle \wedge }$ продолжаются линейно.

Можно проверить, что если мы определим ${\displaystyle [\omega ,\omega ]}$ быть клиновидным продуктом форм, но коммутатор эндоморфизмов в противоположность композиции, то ${\displaystyle \omega \wedge \omega ={\frac {1}{2}}[\omega ,\omega ]}$, и в этих альтернативных обозначениях структурное уравнение Картана принимает вид

${\displaystyle F^{\nabla }=d\omega +{\frac {1}{2}}[\omega ,\omega ].}$

Это альтернативное обозначение обычно используется в теории связностей главных расслоений, где форма связи ${\displaystyle \omega }$ это Алгебра Ли -значная однозначная форма, для которой нет понятия композиции (в отличие от случая эндоморфизмов), но есть понятие скобки Ли.

В некоторых ссылках структурное уравнение Картана может быть записано со знаком минус:

${\displaystyle F^{\nabla }=d\omega -\omega \wedge \omega .}$

В этом другом соглашении используется порядок умножения матриц, отличный от стандартной записи Эйнштейна в произведении клина матричнозначных однозначных форм.

Бьянки идентичность

Версия Бьянки идентичность из римановой геометрии выполняется для связности на любом векторном расслоении. Напомним, что связь ${\displaystyle \nabla }$ на векторном расслоении ${\displaystyle E\to M}$ индуцирует связь эндоморфизма на ${\displaystyle \operatorname {End} (E)}$. Эта связь эндоморфизма имеет внешнюю ковариантную производную, которую мы неоднозначно называем ${\displaystyle d^{\nabla }}$. Поскольку кривизна определяется глобально ${\displaystyle \operatorname {End} (E)}$-значной двумерной формы, мы можем применить к ней внешнюю ковариантную производную. В Бьянки идентичность Говорит, что

${\displaystyle d^{\nabla }F^{\nabla }=0}$.

Это кратко описывает сложные тензорные формулы тождества Бианки в случае римановых многообразий, и можно перейти от этого уравнения к стандартным тождествам Бианки, расширив связь и кривизну в локальных координатах.

Калибровочные преобразования

Смотрите также: Калибровочная группа (математика)

Учитывая две связи ${\displaystyle \nabla _{1},\nabla _{2}}$ на векторном расслоении ${\displaystyle E\to M}$Естественно спросить, когда их можно считать эквивалентными. Существует четко определенное понятие автоморфизм векторного расслоения ${\displaystyle E\to M}$. Секция ${\displaystyle u\in \Gamma (\operatorname {End} (E))}$ является автоморфизмом, если ${\displaystyle u(x)\in \operatorname {End} (E_{x})}$ обратим в каждой точке ${\displaystyle x\in M}$. Такой автоморфизм называется калибровочное преобразование из ${\displaystyle E}$, а группа всех автоморфизмов называется группа датчиков, часто обозначаемый ${\displaystyle {\mathcal {G}}}$ или ${\displaystyle \operatorname {Aut} (E)}$. Группу калибровочных преобразований можно аккуратно охарактеризовать как пространство сечений заглавная A сопряженный пучок ${\displaystyle \operatorname {Ad} ({\mathcal {F}}(E))}$ из комплект кадров векторного расслоения ${\displaystyle E}$. Это не следует путать с строчная а сопряженный пучок ${\displaystyle \operatorname {ad} ({\mathcal {F}}(E))}$, который естественно отождествляется с ${\displaystyle \operatorname {End} (E)}$ сам. Пакет ${\displaystyle \operatorname {Ad} {\mathcal {F}}(E)}$ это связанный пакет в расслоение главных реперов представлением сопряжения ${\displaystyle G=\operatorname {GL} (r)}$ на себя, ${\displaystyle g\mapsto ghg^{-1}}$, и имеет слой той же общей линейной группы ${\displaystyle \operatorname {GL} (r)}$ где ${\displaystyle \operatorname {rank} (E)=r}$. Обратите внимание, что, несмотря на то, что у него такое же волокно, как и в связке кадров ${\displaystyle {\mathcal {F}}(E)}$ и будучи связанным с ним, ${\displaystyle \operatorname {Ad} ({\mathcal {F}}(E))}$ не равно ни расслоению фреймов, ни даже самому главному расслоению. Калибровочную группу можно эквивалентно охарактеризовать как ${\displaystyle {\mathcal {G}}=\Gamma (\operatorname {Ad} {\mathcal {F}}(E)).}$

Калибровочное преобразование ${\displaystyle u}$ из ${\displaystyle E}$ действует по разделам ${\displaystyle s\in \Gamma (E)}$, и поэтому действует на связи путем сопряжения. Явно, если ${\displaystyle \nabla }$ это связь на ${\displaystyle E}$, то определяется ${\displaystyle u\cdot \nabla }$ от

${\displaystyle (u\cdot \nabla )_{X}(s)=u(\nabla _{X}(u^{-1}(s))}$

за ${\displaystyle s\in \Gamma (E),X\in \Gamma (TM)}$. Чтобы проверить это ${\displaystyle u\cdot \nabla }$ соединение, проверяется правило продукта

${\displaystyle {\begin{aligned}u\cdot \nabla (fs)&=u(\nabla (u^{-1}(fs)))\\&=u(\nabla (fu^{-1}(s)))\\&=u(df\otimes u^{-1}(s))+u(f\nabla (u^{-1}(s)))\\&=df\otimes s+fu\cdot \nabla (s).\end{aligned}}}$

Можно проверить, что это определяет левую групповое действие из ${\displaystyle {\mathcal {G}}}$ на аффинном пространстве всех связностей ${\displaystyle {\mathcal {A}}}$.

поскольку ${\displaystyle {\mathcal {A}}}$ является аффинным пространством по образцу ${\displaystyle \Omega ^{1}(M,\operatorname {End} (E))}$, должна существовать некоторая эндоморфизм-значная однозначная форма ${\displaystyle A_{u}\in \Omega ^{1}(M,\operatorname {End} (E))}$ такой, что ${\displaystyle u\cdot \nabla =\nabla +A_{u}}$. Используя определение связи эндоморфизма ${\displaystyle \nabla ^{\operatorname {End} (E)}}$ индуцированный ${\displaystyle \nabla }$, видно, что

${\displaystyle u\cdot \nabla =\nabla -d^{\nabla }(u)u^{-1}}$

то есть ${\displaystyle A_{u}=-d^{\nabla }(u)u^{-1}}$.

Два соединения называются калибровочный эквивалент если они отличаются действием калибровочной группы, и фактор-пространство ${\displaystyle {\mathcal {B}}={\mathcal {A}}/{\mathcal {G}}}$ это пространство модулей всех подключений на ${\displaystyle E}$. В общем случае это топологическое пространство не является ни гладким многообразием, ни даже Пространство Хаусдорфа, но содержит внутри пространство модулей связностей Янга – Миллса на ${\displaystyle E}$, что представляет значительный интерес в калибровочная теория и физика.

Примеры

• Классический ковариантная производная или аффинная связь определяет соединение на касательный пучок из M, или вообще на любом тензорное расслоение образованный взятием тензорного произведения касательного расслоения на себя и дуальное к нему.
• Связь на ${\displaystyle \pi :\mathbb {R} ^{2}\times \mathbb {R} \to \mathbb {R} }$ можно явно описать как оператор

${\displaystyle \nabla =d+{\begin{bmatrix}f_{11}(x)&f_{12}(x)\\f_{21}(x)&f_{22}(x)\end{bmatrix}}dx}$

где ${\displaystyle d}$ - внешняя производная, вычисленная на векторных гладких функциях, а ${\displaystyle f_{ij}(x)}$ гладкие. Секция ${\displaystyle a\in \Gamma (\pi )}$ может быть идентифицирован с картой

${\displaystyle {\begin{cases}\mathbb {R} \to \mathbb {R} ^{2}\\x\mapsto (a_{1}(x),a_{2}(x))\end{cases}}}$

а потом

${\displaystyle \nabla (a)=\nabla {\begin{bmatrix}a_{1}(x)\\a_{2}(x)\end{bmatrix}}={\begin{bmatrix}{\frac {da_{1}(x)}{dx}}+f_{11}(x)a_{1}(x)+f_{12}(x)a_{2}(x)\\{\frac {da_{2}(x)}{dx}}+f_{21}(x)a_{1}(x)+f_{22}(x)a_{2}(x)\end{bmatrix}}dx}$

• Если в пачке есть метрика пакета, внутреннее произведение на его слоях векторного пространства, a метрическое соединение определяется как соединение, совместимое с метрикой связки.
• А Связь Янга-Миллса это особенный метрическое соединение который удовлетворяет Уравнения Янга-Миллса движения.
• А Риманова связь это метрическое соединение на касательном расслоении Риманово многообразие.
• А Леви-Чивита связь является специальной римановой связностью: метрически-совместимой связностью на касательном расслоении, которая также является без кручения. Она уникальна в том смысле, что для любой римановой связности всегда можно найти одну и только одну эквивалентную связь, не имеющую кручения. «Эквивалентный» означает, что он совместим с одной и той же метрикой, хотя тензоры кривизны могут быть разными; увидеть телепараллелизм. Разница между римановой связностью и соответствующей связностью Леви-Чивиты определяется тензор искривления.
• В внешняя производная это плоское соединение на ${\displaystyle E=M\times \mathbb {R} }$ (тривиальное линейное расслоение над M).
• В общем, каноническое плоское соединение есть на любом плоский векторный набор (то есть векторное расслоение, все функции перехода которого постоянны), которое задается внешней производной в любой тривиализации.

Смотрите также

• D-модуль
• Связь (математика)

использованная литература

• Черн, Шиинг-Шэнь (1951), Темы по дифференциальной геометрии, Институт перспективных исследований, конспекты лекций на мимеографе
• Дарлинг, Р. В. Р. (1994), Дифференциальные формы и связи, Кембридж, Великобритания: Издательство Кембриджского университета, ISBN  0-521-46800-0
• Кобаяси, Шошичи; Номидзу, Кацуми (1996) [1963], Основы дифференциальной геометрии, Vol. 1, Библиотека Wiley Classics, Нью-Йорк: Wiley Interscience, ISBN  0-471-15733-3
• Koszul, J. L. (1950), "Homologie et cohomologie des algebres de Lie", Bulletin de la Société Mathématique, 78: 65–127
• Уэллс, Р. (1973), Дифференциальный анализ на комплексных многообразиях, Springer-Verlag, ISBN  0-387-90419-0
• Ambrose, W .; Зингер, И.М. (1953), "Теорема о голономии", Труды Американского математического общества, 75: 428–443, Дои:10.2307/1990721