Обозначение Фойгта - Voigt notation
Эта статья нужны дополнительные цитаты для проверка. (Октябрь 2016) (Узнайте, как и когда удалить этот шаблон сообщения) |
В математика, Обозначение Фойгта или же Форма фойгта в полилинейная алгебра это способ представить симметричный тензор уменьшив его порядок.[1] У этой идеи есть несколько вариантов и связанных названий: Обозначение Манделя, Обозначения Манделя – Фойгта и Нотация Най найдены другие. Обозначение Кельвина это возрождение Хельбига[2] старых идей Лорд Кельвин. Различия здесь заключаются в определенных весах, прикрепленных к выбранным элементам тензора. Номенклатура может варьироваться в зависимости от того, что является традиционным в области применения.
Например, симметричный тензор 2 × 2 Икс имеет только три отдельных элемента: два по диагонали, а другой - вне диагонали. Таким образом, его можно выразить как вектор
- .
Другой пример:
Тензор напряжений (в матричных обозначениях) имеет вид
В нотации Фойгта это упрощено до 6-мерного вектора:
Тензор деформации, аналогичный по своей природе тензору напряжений - оба являются симметричными тензорами второго порядка - задается в матричной форме как
Его представление в обозначениях Фойгта имеет вид
куда , , и инженерные деформации сдвига.
Преимущество использования разных представлений для напряжения и деформации заключается в том, что скалярная инвариантность
сохраняется.
Точно так же трехмерный симметричный тензор четвертого порядка может быть сведен к матрице 6 × 6.
Мнемоническое правило
Простой мнемоническое правило для запоминания нотации Фойгта:
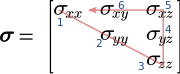
- Запишите тензор второго порядка в матричной форме (в примере - тензор напряжений)
- Вычеркните диагональ
- Продолжайте третью колонку
- Вернитесь к первому элементу в первом ряду.
Индексы Фойгта нумеруются последовательно от начальной точки до конца (в примере цифры синего цвета).
Обозначение Манделя
Для симметричного тензора второго ранга
различны только шесть компонентов, три из которых расположены по диагонали, а остальные - вне диагонали. Таким образом, в обозначениях Манделя можно выразить[3], как вектор
Основное преимущество нотации Манделя состоит в том, что она позволяет использовать те же стандартные операции, которые используются с векторами, например:
Симметричный тензор четвертого ранга, удовлетворяющий и имеет 81 компонент в трехмерном пространстве, но различны только 36 компонентов. Таким образом, в обозначениях Манделя это можно выразить как
Приложения
Обозначение названо в честь физика. Вольдемар Фойгт & Джон Най (ученый). Это полезно, например, в расчетах с использованием конститутивных моделей для моделирования материалов, таких как обобщенные модели. Закон Гука, а также анализ методом конечных элементов,[4] и Диффузная МРТ.[5]
Закон Гука имеет симметричный тензор жесткости четвертого порядка с 81 компонентом (3 × 3 × 3 × 3), но поскольку применение такого тензора ранга 4 к симметричному тензору ранга 2 должно дать другой симметричный тензор ранга 2, не все из 81 элемента независимы. Нотация Фойгта позволяет такому тензору ранга 4 быть представлен матрицей 6 × 6. Однако форма Фойгта не сохраняет сумму квадратов, которая в случае закона Гука имеет геометрическое значение. Это объясняет, почему вводятся веса (чтобы сделать отображение изометрия ).
Обсуждение инвариантности обозначений Фойгта и обозначений Манделя можно найти в Helnwein (2001).[6]
Рекомендации
- ^ Вольдемар Фойгт (1910). Lehrbuch der kristallphysik. Тойбнер, Лейпциг. Получено 29 ноября, 2016.
- ^ Клаус Хельбиг (1994). Основы анизотропии для разведочной сейсмики. Пергамон. ISBN 0-08-037224-4.
- ^ Жан Мандель (1965). "Généralisation de la theorie de plasticité de WT Koiter". Международный журнал твердых тел и структур. 1 (3): 273–295. Дои:10.1016 / 0020-7683 (65) 90034-х.
- ^ O.C. Зенкевич; Р.Л. Тейлор; J.Z. Чжу (2005). Метод конечных элементов: его основы и основы (6 изд.). Эльзевьер Баттерворт - Хайнеманн. ISBN 978-0-7506-6431-8.
- ^ Махер Мохер (2009). «Алгебра тензоров четвертого порядка с приложением к диффузионной МРТ». Визуализация и обработка тензорных полей. Математика и визуализация. Springer Berlin Heidelberg. С. 57–80. Дои:10.1007/978-3-540-88378-4_4. ISBN 978-3-540-88377-7.
- ^ Питер Хельнвайн (16 февраля 2001 г.). «Некоторые замечания о сжатом матричном представлении симметричных тензоров второго и четвертого порядков». Компьютерные методы в прикладной механике и технике. 190 (22–23): 2753–2770. Bibcode:2001CMAME.190.2753H. Дои:10.1016 / с0045-7825 (00) 00263-2.


![{ boldsymbol { sigma}} = left [{{ begin {matrix} sigma _ {{xx}} & sigma _ {{xy}} & sigma _ {{xz}} sigma _ {{yx}} & sigma _ {{yy}} & sigma _ {{yz}} sigma _ {{zx}} & sigma _ {{zy}} & sigma _ {{zz} } end {matrix}}} right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/7a3b47956f327717849940e2eddd177e6a135b9a)

![{ boldsymbol { epsilon}} = left [{{ begin {matrix} epsilon _ {{xx}} & epsilon _ {{xy}} & epsilon _ {{xz}} epsilon _ {{yx}} & epsilon _ {{yy}} & epsilon _ {{yz}} epsilon _ {{zx}} & epsilon _ {{zy}} & epsilon _ {{zz} } end {matrix}}} right].](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a87e30950dffdfd48d25069ee1ec1d5e659ada9)





![{ boldsymbol { sigma}} = left [{{ begin {matrix} sigma _ {{11}} & sigma _ {{12}} & sigma _ {{13}} sigma _ {{21}} & sigma _ {{22}} & sigma _ {{23}} sigma _ {{31}} & sigma _ {{32}} & sigma _ {{33} } end {matrix}}} right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/f6013e0552a56a7a266e368145fb181089da6838)




