Формулировка интеграла по путям - Path integral formulation - Wikipedia

Эта статья посвящена формулировке квантовой механики. Для интегралов вдоль пути, также известных как линейные или контурные интегралы, см. линейный интеграл.

В формулировка интеграла по путям это описание в квантовая механика это обобщает принцип действия из классическая механика. Он заменяет классическое понятие единственной уникальной классической траектории для системы суммой, или функциональный интеграл, по бесконечному количеству возможных квантово-механических траекторий для вычисления квантовая амплитуда.

Эта формулировка оказалась решающей для последующего развития теоретическая физика, потому что манифест Ковариация Лоренца (временные и пространственные компоненты величин входят в уравнения таким же образом) добиться легче, чем в операторном формализме каноническое квантование. В отличие от предыдущих методов, интеграл по путям позволяет легко изменять координаты между очень разными канонический описания одной и той же квантовой системы. Еще одно преимущество заключается в том, что на практике легче угадать правильную форму Лагранжиан теории, которая естественным образом входит в интегралы по путям (для взаимодействий определенного типа это координатное пространство или же Интегралы по траекториям Фейнмана), чем Гамильтониан. Возможные недостатки подхода включают следующее: унитарность (это связано с сохранением вероятности; вероятности всех физически возможных результатов должны составлять в сумме один) S-матрица неясно в формулировке. Доказано, что подход интеграла по путям эквивалентен другим формализмам квантовой механики и квантовой теории поля. Таким образом, получение при переходе к другому подходу проблемы, связанные с тем или иным подходом (на примере лоренцевской ковариантности или унитарности), исчезают.^[1]

Интеграл по путям также связывает квантовую и стохастический процессов, и это послужило основой для великого синтеза 1970-х годов, который объединил квантовая теория поля с статистическая теория поля флуктуирующего поля около фазовый переход второго рода. В Уравнение Шредингера это уравнение диффузии с мнимой постоянной диффузии, а интеграл по путям представляет собой аналитическое продолжение метода суммирования всех возможных случайные прогулки.^[2]

Основная идея формулировки интеграла по путям восходит к Норберт Винер, который представил Винеровский интеграл для решения проблем в области распространения и Броуновское движение.^[3] Эта идея была распространена на использование Лагранжиан в квантовой механике Поль Дирак в своей статье 1933 года.^[4][5] Полный метод был разработан в 1948 г. Ричард Фейнман. Некоторые предварительные задания были разработаны ранее в его докторской работе под руководством Джон Арчибальд Уиллер. Первоначальная мотивация проистекала из желания получить квантово-механическую формулировку для Теория поглотителя Уиллера – Фейнмана используя Лагранжиан (а не Гамильтониан ) в качестве отправной точки.

Это пять из бесконечного множества путей, доступных для частицы, чтобы двигаться из точки A в момент времени t в точку B в момент времени t ’(> t). Пути, которые пересекаются друг с другом или идут в обратном направлении, не допускаются.

Принцип квантового действия

В квантовой механике, как и в классической механике, Гамильтониан генератор временных трансляций. Это означает, что состояние в несколько более позднее время отличается от состояния в текущий момент результатом действия с оператором Гамильтона (умноженным на отрицательное мнимая единица, −я). Для состояний с определенной энергией это утверждение соотношение де Бройля между частотой и энергией, и общее соотношение согласуется с этим плюс принцип суперпозиции.

Гамильтониан в классической механике выводится из Лагранжиан, которая является более фундаментальной величиной по сравнению с специальная теория относительности. Гамильтониан указывает, как двигаться вперед во времени, но время отличается в разных системы отсчета. Лагранжиан - это Скаляр Лоренца, а гамильтониан - это временная составляющая четырехвекторный. Таким образом, гамильтониан отличается в разных системах отсчета, и этот тип симметрии не проявляется в исходной формулировке квантовой механики.

Гамильтониан является функцией положения и импульса в один момент времени, и он определяет положение и импульс немного позже. Лагранжиан является функцией текущего положения и положения несколько позже (или, что эквивалентно для бесконечно малых временных интервалов, он является функцией положения и скорости). Отношения между этими двумя Превращение Лежандра, и условие, определяющее классические уравнения движения ( Уравнения Эйлера – Лагранжа. ) заключается в том, что действие имеет экстремум.

В квантовой механике преобразование Лежандра трудно интерпретировать, потому что движение не идет по определенной траектории. В классической механике с дискретизация со временем преобразование Лежандра становится

${\displaystyle \varepsilon H=p(t){\big (}q(t+\varepsilon )-q(t){\big )}-\varepsilon L}$

и

${\displaystyle p={\frac {\partial L}{\partial {\dot {q}}}},}$

где частная производная по ${\displaystyle {\dot {q}}}$ держит q(т + ε) фиксированный. Обратное преобразование Лежандра имеет вид

${\displaystyle \varepsilon L=\varepsilon p{\dot {q}}-\varepsilon H,}$

куда

${\displaystyle {\dot {q}}={\frac {\partial H}{\partial p}},}$

и частная производная теперь по п при фиксированном q.

В квантовой механике состояние - это суперпозиция разных состояний с разными значениями q, или разные значения п, а величины п и q можно интерпретировать как некоммутирующие операторы. Оператор п определен только на состояниях, неопределенных относительно q. Итак, рассмотрим два состояния, разделенных во времени, и действуем с оператором, соответствующим лагранжиану:

${\displaystyle e^{i{\big [}p{\big (}q(t+\varepsilon )-q(t){\big )}-\varepsilon H(p,q){\big ]}}.}$

Если умножения, неявные в этой формуле, интерпретируются как матрица умножения, первый множитель

${\displaystyle e^{-ipq(t)},}$

и если это также интерпретируется как умножение матриц, сумма по всем состояниям интегрируется по всем q(т), и поэтому требуется преобразование Фурье в q(т) изменить базу на п(т). Это действие в гильбертовом пространстве - изменить основу на п вовремя т.

Далее идет

${\displaystyle e^{-i\varepsilon H(p,q)},}$

или же развить бесконечно малое время в будущее.

Наконец, последний фактор в этой интерпретации -

${\displaystyle e^{ipq(t+\varepsilon )},}$

что значит изменить основу обратно на q позже.

Это не сильно отличается от обычной временной эволюции: ЧАС factor содержит всю динамическую информацию - продвигает состояние вперед во времени. Первая и последняя части - это просто преобразования Фурье, чтобы перейти к чистому q основа из промежуточного п основание.

... мы видим, что подынтегральное выражение в (11) должно иметь вид е^{если/час}, куда F является функцией q_Т, q₁, q₂, … q_м, q_т, который остается конечным при час стремится к нулю. Давайте теперь изобразим одну из промежуточных qс, скажи q_k, как постоянно меняющиеся, в то время как другие фиксированы. Из-за малости час, то в общем случае F/час меняется очень быстро. Это означает, что е^{если/час} будет периодически меняться с очень высокой частотой около нулевого значения, в результате чего его интеграл будет практически нулевым. Единственная важная часть в области интеграции q_k таким образом, для которого существует сравнительно большой разброс в q_k производит лишь очень небольшое изменение в F. Эта часть является окрестностью точки, для которой F стационарен относительно малых изменений q_k. Мы можем применить этот аргумент к каждой из переменных интегрирования ... и получить результат, что единственной важной частью в области интегрирования является та, для которой F является стационарным для небольших изменений во всех промежуточных qс. ... Мы видим, что F имеет своим классическим аналогом ∫^т
_Т L dt, которая является просто функцией действия, которую классическая механика требует, чтобы она была стационарной при малых изменениях всех промежуточных qс. Это показывает, каким образом уравнение (11) переходит в классические результаты, когда час становится очень маленьким.

Дирак (1933), стр. 69

Другой способ сказать это: поскольку гамильтониан естественным образом является функцией п и q, возведя в степень это количество и изменив базис с п к q на каждом шаге позволяет матричный элемент ЧАС для выражения в виде простой функции на каждом пути. Эта функция является квантовым аналогом классического действия. Это наблюдение связано с Поль Дирак.^[6]

Дирак далее отметил, что можно возвести в квадрат оператор эволюции во времени в S представление:

${\displaystyle e^{i\varepsilon S},}$

и это дает оператор временной эволюции между временем т и время т + 2ε. Пока в ЧАС Представление суммы, которая суммируется по промежуточным состояниям, является неясным матричным элементом в S представление, это переосмысливается как величина, связанная с путем. В пределе, когда этот оператор принимает большую степень, восстанавливается полная квантовая эволюция между двумя состояниями, первое - с фиксированным значением q(0) а второй с фиксированным значением q(т). Результатом является сумма по путям с фазой, которая является квантовым действием. Важно отметить, что в этой статье Дирак выявил глубокую квантово-механическую причину принцип наименьшего действия контроль классического предела (см. цитату).

Интерпретация Фейнмана

Работа Дирака не давала точного рецепта для вычисления суммы по путям, и он не показал, что можно восстановить уравнение Шредингера или канонические коммутационные соотношения из этого правила. Это сделал Фейнман.^{[nb 1]} То есть классический путь естественным образом возникает в классическом пределе.

Фейнман показал, что квантовое действие Дирака для большинства интересных случаев просто равно классическому действию, соответствующим образом дискретизированному. Это означает, что классическое действие - это фаза, полученная в результате квантовой эволюции между двумя фиксированными конечными точками. Он предложил восстановить всю квантовую механику из следующих постулатов:

1. В вероятность для события дается квадратом модуля комплексного числа, называемого «амплитудой вероятности».
2. В амплитуда вероятности дается сложением вкладов всех путей в конфигурационном пространстве.
3. Вклад пути пропорционален е^{является/час}, куда S это действие предоставленный интеграл по времени из Лагранжиан по пути.

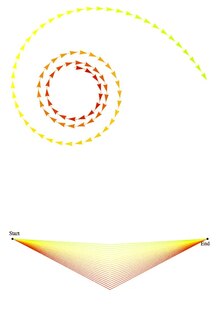
Затем, чтобы найти общую амплитуду вероятности для данного процесса, складывается, или объединяет, амплитуда 3-го постулата в пространстве все возможные пути системы между начальным и конечным состояниями, в том числе абсурдные по классическим меркам. При вычислении амплитуды вероятности перехода отдельной частицы от одной пространственно-временной координаты к другой, правильно включать пути, по которым частица описывает сложные завитушки, кривые, в которых частица вылетает в космическое пространство и снова летит обратно, и так далее. В интеграл по путям присваивает всем этим амплитудам равный вес но разные фаза, или аргумент комплексное число. Вклады от путей, сильно отличающихся от классической траектории, могут быть подавлены вмешательство (Смотри ниже).

Фейнман показал, что эта формулировка квантовой механики эквивалентна формулировке канонический подход к квантовой механике когда гамильтониан не более чем квадратичен по импульсу. Амплитуда, вычисленная в соответствии с принципами Фейнмана, также будет подчиняться Уравнение Шредингера для Гамильтониан соответствующему данному действию.

Формулировка интеграла по путям квантовой теории поля представляет собой амплитуда перехода (соответствует классическому корреляционная функция ) как взвешенную сумму всех возможных историй системы от начального до конечного состояния. А Диаграмма Фейнмана является графическим представлением пертурбативный вклад в амплитуду перехода.

Интеграл по путям в квантовой механике

Вывод с квантованием времени

Основная статья: Связь между уравнением Шредингера и формулировкой интеграла по путям квантовой механики

Один из распространенных подходов к выводу формулы интеграла по путям - разделение временного интервала на небольшие части. Как только это будет сделано, Формула продукта Trotter говорит нам, что некоммутативностью операторов кинетической и потенциальной энергии можно пренебречь.

Для частицы в гладком потенциале интеграл по путям аппроксимируется формулой зигзаг пути, которые в одном измерении являются произведением обычных интегралов. Для движения частицы из положения Икс_а вовремя т_а к Икс_б вовремя т_б, временная последовательность

${\displaystyle t_{a}=t_{0}<t_{1}<\cdots <t_{n-1}<t_{n}<t_{n+1}=t_{b}}$

можно разделить на п + 1 меньшие сегменты т_j − т_{j − 1}, куда j = 1, ..., п + 1, фиксированной продолжительности

${\displaystyle \varepsilon =\Delta t={\frac {t_{b}-t_{a}}{n+1}}.}$

Этот процесс называется временные интервалы.

Приближение для интеграла по путям можно вычислить как пропорциональное

${\displaystyle \int \limits _{-\infty }^{+\infty }\cdots \int \limits _{-\infty }^{+\infty }\exp \left({\frac {i}{\hbar }}\int _{t_{a}}^{t_{b}}L{\big (}x(t),v(t){\big )}\,dt\right)\,dx_{0}\,\cdots \,dx_{n},}$

куда L(Икс, v) - лагранжиан одномерной системы с позиционной переменной Икс(т) и скорость v = Икс(т) рассматривается (см. ниже), и dx_j соответствует положению на j-й шаг по времени, если интеграл по времени аппроксимируется суммой п термины.^{[nb 2]}

В пределе п → ∞, это становится функциональный интеграл, который, помимо несущественного фактора, является прямым произведением амплитуд вероятностей ⟨Икс_б, т_б|Икс_а, т_а⟩ (точнее, поскольку нужно работать с непрерывным спектром, с соответствующими плотностями), чтобы найти квантово-механическую частицу в точке т_а в исходном состоянии Икс_а и в т_б в конечном состоянии Икс_б.

Фактически L классический Лагранжиан рассматриваемой одномерной системы,

${\displaystyle L(x,{\dot {x}})=T-V={\frac {1}{2}}m|{\dot {x}}|^{2}-V(x)}$

и упомянутый выше "зигзаг" соответствует появлению терминов

${\displaystyle \exp \left({\frac {i}{\hbar }}\varepsilon \sum _{j=1}^{n+1}L\left({\tilde {x}}_{j},{\frac {x_{j}-x_{j-1}}{\varepsilon }},j\right)\right)}$

в Сумма Римана аппроксимирующие интеграл по времени, которые окончательно интегрируются по Икс₁ к Икс_п с мерой интегрирования dx₁...dx_п, Икс_j - произвольное значение интервала, соответствующего j, например его центр, Икс_j + Икс_j−1/2.

Таким образом, в отличие от классической механики, вклад вносит не только стационарный путь, но и фактически все виртуальные пути между начальной и конечной точкой.

Формула интеграла по путям

В терминах волновой функции в позиционном представлении формула интеграла по путям выглядит следующим образом:

${\displaystyle \psi (x,t)={\frac {1}{Z}}\int _{\mathbf {x} (0)=x}{\mathcal {D}}\mathbf {x} \,e^{iS[\mathbf {x} ,{\dot {\mathbf {x} }}]}\psi _{0}(\mathbf {x} (t))\,}$

куда ${\displaystyle {\mathcal {D}}\mathbf {x} }$ обозначает интеграцию по всем путям ${\displaystyle \mathbf {x} }$ с ${\displaystyle \mathbf {x} (0)=x}$ и где ${\displaystyle Z}$ коэффициент нормализации. Здесь ${\displaystyle S}$ это действие, заданное

${\displaystyle S[\mathbf {x} ,{\dot {\mathbf {x} }}]=\int dt\,L(\mathbf {x} (t),{\dot {\mathbf {x} }}(t))}$

Воспроизвести медиа

На диаграмме показан вклад в интеграл по путям свободной частицы для набора траекторий.

Бесплатная частица

Представление интеграла по путям дает квантовую амплитуду для выхода из точки Икс В точку у как интеграл по всем путям. Для действия свободной частицы (для простоты пусть м = 1, час = 1)

${\displaystyle S=\int {\frac {{\dot {x}}^{2}}{2}}\,dt,}$

интеграл можно вычислить явно.

Для этого удобно начать без фактора я в экспоненте, так что большие отклонения подавляются малыми числами, а не сокращением колебательных вкладов. Амплитуда (или ядро) гласит:

${\displaystyle K(x-y;T)=\int _{x(0)=x}^{x(T)=y}\exp \left(-\int _{0}^{T}{\frac {{\dot {x}}^{2}}{2}}\,dt\right)\,Dx.}$

Разбиение интеграла на временные отрезки:

${\displaystyle K(x,y;T)=\int _{x(0)=x}^{x(T)=y}\prod _{t}\exp \left(-{\tfrac {1}{2}}\left({\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}\right)^{2}\varepsilon \right)\,Dx,}$

где Dx интерпретируется как конечный набор интеграций в каждом целом кратном ε. Каждый фактор в произведении является гауссовским как функция Икс(т + ε) сосредоточен на Икс(т) с отклонением ε. Кратные интегралы повторяются свертка этого гауссовского грамм_ε с копиями самого себя в соседнее время:

${\displaystyle K(x-y;T)=G_{\varepsilon }*G_{\varepsilon }*\cdots *G_{\varepsilon },}$

где количество витков Т/ε. Результат легко оценить, взяв преобразование Фурье обеих сторон, так что свертки становятся умножениями:

${\displaystyle {\tilde {K}}(p;T)={\tilde {G}}_{\varepsilon }(p)^{T/\varepsilon }.}$

Преобразование Фурье гауссовского грамм - еще один гауссиан обратной дисперсии:

${\displaystyle {\tilde {G}}_{\varepsilon }(p)=e^{-{\frac {\varepsilon p^{2}}{2}}},}$

и результат

${\displaystyle {\tilde {K}}(p;T)=e^{-{\frac {Tp^{2}}{2}}}.}$

Преобразование Фурье дает K, и это снова гауссиан с обратной дисперсией:

${\displaystyle K(x-y;T)\propto e^{-{\frac {(x-y)^{2}}{2T}}}.}$

Константа пропорциональности на самом деле не определяется подходом с квантованием времени, определяется только соотношение значений для различных вариантов конечной точки. Константу пропорциональности следует выбирать так, чтобы гарантировать, что между каждыми двумя временными отрезками эволюция во времени является квантово-механически унитарной, но более понятный способ исправить нормализацию - это рассматривать интеграл по путям как описание случайного процесса.

Результат имеет вероятностную интерпретацию. Сумму по всем путям экспоненциального фактора можно рассматривать как сумму по каждому пути вероятности выбора этого пути. Вероятность - это произведение по каждому сегменту вероятности выбора этого сегмента, так что каждый сегмент выбирается вероятностно независимо. Тот факт, что ответом является гауссово линейное расширение во времени, является Центральная предельная теорема, который можно интерпретировать как первую историческую оценку статистического интеграла по траектории.

Вероятностная интерпретация дает естественный выбор нормализации. Интеграл по путям следует определять так, чтобы

${\displaystyle \int K(x-y;T)\,dy=1.}$

Это условие нормализует гауссиану и дает ядро, которое подчиняется уравнению диффузии:

${\displaystyle {\frac {d}{dt}}K(x;T)={\frac {\nabla ^{2}}{2}}K.}$

Для осциллирующих интегралов по траекториям интегралы с я в числителе квантование времени дает свернутые гауссианы, как и раньше. Однако теперь свертка является незначительно сингулярной, поскольку требует точных ограничений для вычисления осциллирующих интегралов. Чтобы факторы были четко определены, проще всего добавить небольшую мнимую часть к временному приращению. ε. Это тесно связано с Вращение фитиля. Затем тот же аргумент свертки, что и раньше, дает ядро ​​распространения:

${\displaystyle K(x-y;T)\propto e^{\frac {i(x-y)^{2}}{2T}},}$

которое с той же нормализацией, что и раньше (не нормализация на сумму квадратов - эта функция имеет расходящуюся норму), подчиняется свободному уравнению Шредингера:

${\displaystyle {\frac {d}{dt}}K(x;T)=i{\frac {\nabla ^{2}}{2}}K.}$

Это означает, что любая суперпозиция Ks также будет подчиняться тому же уравнению по линейности. Определение

${\displaystyle \psi _{t}(y)=\int \psi _{0}(x)K(x-y;t)\,dx=\int \psi _{0}(x)\int _{x(0)=x}^{x(t)=y}e^{iS}\,Dx,}$

тогда ψ_т подчиняется свободному уравнению Шредингера так же, как K делает:

${\displaystyle i{\frac {\partial }{\partial t}}\psi _{t}=-{\frac {\nabla ^{2}}{2}}\psi _{t}.}$

Простой гармонический осциллятор

Лагранжиан для простого гармонического осциллятора имеет вид^[7]

${\displaystyle {\mathcal {L}}={\tfrac {1}{2}}m{\dot {x}}^{2}-{\tfrac {1}{2}}m\omega ^{2}x^{2}.}$

Напишите его траекторию Икс(т) как классическая траектория плюс некоторое возмущение, Икс(т) = Икс_c(т) + δx(т) и действие как S = S_c + δS. Классическую траекторию можно записать как

${\displaystyle x_{\text{c}}(t)=x_{i}{\frac {\sin \omega (t_{f}-t)}{\sin \omega (t_{f}-t_{i})}}+x_{f}{\frac {\sin \omega (t-t_{i})}{\sin \omega (t_{f}-t_{i})}}.}$

Эта траектория дает классическое действие

${\displaystyle {\begin{aligned}S_{\text{c}}&=\int _{t_{i}}^{t_{f}}{\mathcal {L}}\,dt=\int _{t_{i}}^{t_{f}}\left({\tfrac {1}{2}}m{\dot {x}}^{2}-{\tfrac {1}{2}}m\omega ^{2}x^{2}\right)\,dt\\[6pt]&={\frac {1}{2}}m\omega \left({\frac {(x_{i}^{2}+x_{f}^{2})\cos \omega (t_{f}-t_{i})-2x_{i}x_{f}}{\sin \omega (t_{f}-t_{i})}}\right)~.\end{aligned}}}$

Затем разложите отклонение от классического пути в ряд Фурье и вычислите вклад в действие δS, который дает

${\displaystyle S=S_{\text{c}}+\sum _{n=1}^{\infty }{\tfrac {1}{2}}a_{n}^{2}{\frac {m}{2}}\left({\frac {(n\pi )^{2}}{t_{f}-t_{i}}}-\omega ^{2}(t_{f}-t_{i})\right).}$

Это означает, что пропагатор

${\displaystyle {\begin{aligned}K(x_{f},t_{f};x_{i},t_{i})&=Qe^{\frac {iS_{\text{c}}}{\hbar }}\prod _{j=1}^{\infty }{\frac {j\pi }{\sqrt {2}}}\int da_{j}\exp {\left({\frac {i}{2\hbar }}a_{j}^{2}{\frac {m}{2}}\left({\frac {(j\pi )^{2}}{t_{f}-t_{i}}}-\omega ^{2}(t_{f}-t_{i})\right)\right)}\\[6pt]&=e^{\frac {iS_{\text{c}}}{\hbar }}Q\prod _{j=1}^{\infty }\left(1-\left({\frac {\omega (t_{f}-t_{i})}{j\pi }}\right)^{2}\right)^{-{\frac {1}{2}}}\end{aligned}}}$

для некоторой нормализации

${\displaystyle Q={\sqrt {\frac {m}{2\pi i\hbar (t_{f}-t_{i})}}}~.}$

Используя представление бесконечного произведения функция sinc,

${\displaystyle \prod _{j=1}^{\infty }\left(1-{\frac {x^{2}}{j^{2}}}\right)={\frac {\sin \pi x}{\pi x}},}$

пропагатор можно записать как

${\displaystyle K(x_{f},t_{f};x_{i},t_{i})=Qe^{\frac {iS_{\text{c}}}{\hbar }}{\sqrt {\frac {\omega (t_{f}-t_{i})}{\sin \omega (t_{f}-t_{i})}}}=e^{\frac {iS_{c}}{\hbar }}{\sqrt {\frac {m\omega }{2\pi i\hbar \sin \omega (t_{f}-t_{i})}}}.}$

Позволять Т = т_ж − т_я. Этот пропагатор в терминах собственных состояний энергии можно записать как

${\displaystyle {\begin{aligned}K(x_{f},t_{f};x_{i},t_{i})&=\left({\frac {m\omega }{2\pi i\hbar \sin \omega T}}\right)^{\frac {1}{2}}\exp {\left({\frac {i}{\hbar }}{\tfrac {1}{2}}m\omega {\frac {(x_{i}^{2}+x_{f}^{2})\cos \omega T-2x_{i}x_{f}}{\sin \omega T}}\right)}\\[6pt]&=\sum _{n=0}^{\infty }\exp {\left(-{\frac {iE_{n}T}{\hbar }}\right)}\psi _{n}(x_{f})\psi _{n}(x_{i})^{*}~.\end{aligned}}}$

Использование идентичностей я грех ωT = 1/2е^iωT (1 − е^−2iωT) и потому что ωT = 1/2е^iωT (1 + е^−2iωT), это составляет

${\displaystyle K(x_{f},t_{f};x_{i},t_{i})=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{2}}e^{\frac {-i\omega T}{2}}\left(1-e^{-2i\omega T}\right)^{-{\frac {1}{2}}}\exp {\left(-{\frac {m\omega }{2\hbar }}\left(\left(x_{i}^{2}+x_{f}^{2}\right){\frac {1+e^{-2i\omega T}}{1-e^{-2i\omega T}}}-{\frac {4x_{i}x_{f}e^{-i\omega T}}{1-e^{-2i\omega T}}}\right)\right)}.}$

Можно поглотить все термины после первого е^−iωT/2 в р(Т), тем самым получив

${\displaystyle K(x_{f},t_{f};x_{i},t_{i})=\left({\frac {m\omega }{\pi \hbar }}\right)^{\frac {1}{2}}e^{\frac {-i\omega T}{2}}\cdot R(T).}$

Наконец-то можно расширить р(Т) в полномочиях е^−iωT: Все термины в этом расширении умножаются на е^−iωT/2 фактор спереди, давая условия формы

${\displaystyle e^{\frac {-i\omega T}{2}}e^{-in\omega T}=e^{-i\omega T\left({\frac {1}{2}}+n\right)}\quad {\text{for }}n=0,1,2,\ldots .}$

Сравнение с приведенным выше разложением по собственным состояниям дает стандартный энергетический спектр для простого гармонического осциллятора,

${\displaystyle E_{n}=\left(n+{\tfrac {1}{2}}\right)\hbar \omega ~.}$

Смотрите также: Пропагатор § Основные примеры: пропагатор свободной частицы и гармонический осциллятор, и Ядро Мелера

Кулоновский потенциал

Однако приближение Фейнмана с временным разрезом не существует для наиболее важных квантово-механических интегралов по траекториям атомов из-за сингулярности Кулоновский потенциал е²/р в происхождении. Только после замены времени т другим параметром псевдовремени, зависящим от пути

${\displaystyle s=\int {\frac {dt}{r(t)}}}$

сингулярность удаляется, и существует приближение с временным разрезом, которое является точно интегрируемым, поскольку его можно сделать гармоническим с помощью простого преобразования координат, как было обнаружено в 1979 г. Исмаил Хакки Дуру и Хаген Кляйнерт.^[8] Комбинация преобразования времени, зависящего от траектории, и преобразования координат является важным инструментом для решения многих интегралов по траектории и обычно называется Преобразование Дуру – Клейнерта.

Уравнение Шредингера

Основная статья: Связь между уравнением Шредингера и формулировкой интеграла по путям квантовой механики

Интеграл по путям воспроизводит уравнение Шредингера для начального и конечного состояния даже при наличии потенциала. Это легче всего увидеть, взяв интеграл по путям за бесконечно малые промежутки времени.

${\displaystyle \psi (y;t+\varepsilon )=\int _{-\infty }^{\infty }\psi (x;t)\int _{x(t)=x}^{x(t+\varepsilon )=y}e^{i\int \limits _{t}^{t+\varepsilon }\left({\frac {{\dot {x}}^{2}}{2}}-V(x)\right)\,dt}\,Dx(t)\,dx\qquad (1)}$

Поскольку временное разделение бесконечно мало и компенсирующие колебания становятся сильными для больших значений Икс, интеграл по путям имеет наибольший вес при у рядом с Икс. В этом случае до низшего порядка потенциальная энергия постоянна, и только вклад кинетической энергии нетривиален. (Это разделение членов кинетической и потенциальной энергии в показателе экспоненты по существу является Формула продукта Trotter.) Экспонента действия равна

${\displaystyle e^{-i\varepsilon V(x)}e^{i{\frac {{\dot {x}}^{2}}{2}}\varepsilon }}$

Первый член вращает фазу ψ(Икс) локально на величину, пропорциональную потенциальной энергии. Второй член - пропагатор свободной частицы, соответствующий я раз процесс диффузии. В самый низкий порядок в ε они аддитивны; в любом случае с (1):

${\displaystyle \psi (y;t+\varepsilon )\approx \int \psi (x;t)e^{-i\varepsilon V(x)}e^{\frac {i(x-y)^{2}}{2\varepsilon }}\,dx\,.}$

Как уже упоминалось, разброс в ψ является диффузным из-за распространения свободных частиц с дополнительным бесконечно малым вращением фазы, которое медленно изменяется от точки к точке в зависимости от потенциала:

${\displaystyle {\frac {\partial \psi }{\partial t}}=i\cdot \left({\tfrac {1}{2}}\nabla ^{2}-V(x)\right)\psi \,}$

и это уравнение Шредингера. Нормировку интеграла по путям необходимо зафиксировать точно так же, как и в случае свободных частиц. Произвольный непрерывный потенциал не влияет на нормализацию, хотя сингулярные потенциалы требуют осторожного обращения.

Уравнения движения

Поскольку состояния подчиняются уравнению Шредингера, интеграл по путям должен воспроизводить уравнения движения Гейзенберга для средних значений Икс и Икс переменные, но поучительно увидеть это напрямую. Прямой подход показывает, что математические ожидания, вычисленные с помощью интеграла по путям, воспроизводят обычные значения квантовой механики.

Начнем с рассмотрения интеграла по путям с некоторым фиксированным начальным состоянием

${\displaystyle \int \psi _{0}(x)\int _{x(0)=x}e^{iS(x,{\dot {x}})}\,Dx\,}$

Сейчас же Икс(т) в каждый отдельный момент времени - отдельная переменная интегрирования. Таким образом, можно изменять переменные в интеграле путем сдвига: Икс(т) = ты(т) + ε(т) куда ε(т) это разные смены каждый раз, но ε(0) = ε(Т) = 0, поскольку конечные точки не интегрированы:

${\displaystyle \int \psi _{0}(x)\int _{u(0)=x}e^{iS(u+\varepsilon ,{\dot {u}}+{\dot {\varepsilon }})}\,Du\,}$

Изменение интеграла от сдвига до первого бесконечно малого порядка по ε:

${\displaystyle \int \psi _{0}(x)\int _{u(0)=x}\left(\int {\frac {\partial S}{\partial u}}\varepsilon +{\frac {\partial S}{\partial {\dot {u}}}}{\dot {\varepsilon }}\,dt\right)e^{iS}\,Du\,}$

которые, интегрируя по частям в т, дает:

${\displaystyle \int \psi _{0}(x)\int _{u(0)=x}-\left(\int \left({\frac {d}{dt}}{\frac {\partial S}{\partial {\dot {u}}}}-{\frac {\partial S}{\partial u}}\right)\varepsilon (t)\,dt\right)e^{iS}\,Du\,}$

Но это был просто сдвиг переменных интегрирования, который не меняет значения интеграла при любом выборе ε(т). Вывод состоит в том, что это изменение первого порядка равно нулю для произвольного начального состояния и в любой произвольный момент времени:

${\displaystyle \left\langle \psi _{0}\left|{\frac {\delta S}{\delta x}}(t)\right|\psi _{0}\right\rangle =0}$

это уравнение движения Гейзенберга.

Если в действии есть члены, умножающие Икс и Икс, в тот же момент времени, описанные выше манипуляции являются лишь эвристическими, потому что правила умножения для этих величин так же некоммутируют в интеграле по путям, как и в операторном формализме.

Приближение стационарной фазы

Если вариация действия превышает час на много порядков величины мы обычно имеем деструктивную интерференцию помимо тех траекторий, которые удовлетворяют Уравнение Эйлера – Лагранжа., которое теперь интерпретируется как условие конструктивного вмешательства. Это можно показать с помощью метода стационарной фазы, примененного к пропагатору. В качестве час убывает, экспонента в интеграле быстро осциллирует в комплексной области при любом изменении действия. Таким образом, в пределе час стремится к нулю, только те точки, где классическое действие не меняется, вносят вклад в пропагатор.

Канонические коммутационные соотношения

Формулировка интеграла по путям на первый взгляд не дает понять, что величины Икс и п не ездить на работу. В интеграле по путям это просто переменные интегрирования, и они не имеют очевидного порядка. Фейнман обнаружил, что некоммутативность все еще присутствует.^[9]

Чтобы убедиться в этом, рассмотрим простейший интеграл по путям - броуновское блуждание. Это еще не квантовая механика, поэтому в интеграле по путям действие не умножается на я:

${\displaystyle S=\int \left({\frac {dx}{dt}}\right)^{2}\,dt}$

Количество Икс(т) колеблется, а производная определяется как предел дискретной разности.

${\displaystyle {\frac {dx}{dt}}={\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}}$

Расстояние, которое проходит случайное блуждание, пропорционально √т, так что:

${\displaystyle x(t+\varepsilon )-x(t)\approx {\sqrt {\varepsilon }}}$

Это показывает, что случайное блуждание не дифференцируемо, так как отношение, определяющее производную, расходится с вероятностью единица.

Количество xẋ неоднозначно, имеет два возможных значения:

${\displaystyle [1]=x{\frac {dx}{dt}}=x(t){\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}}$

${\displaystyle [2]=x{\frac {dx}{dt}}=x(t+\varepsilon ){\frac {x(t+\varepsilon )-x(t)}{\varepsilon }}}$

В элементарном исчислении они различаются только величиной, равной 0, как ε переходит в 0. Но в этом случае разница между ними не равна 0:

${\displaystyle [2]-[1]={\frac {{\big (}x(t+\varepsilon )-x(t){\big )}^{2}}{\varepsilon }}\approx {\frac {\varepsilon }{\varepsilon }}}$

Позволять

${\displaystyle f(t)={\frac {{\big (}x(t+\varepsilon )-x(t){\big )}^{2}}{\varepsilon }}}$

потом ж(т) - быстро флуктуирующая статистическая величина, среднее значение которой равно 1, то есть нормализованный «гауссовский процесс». Колебания такой величины можно описать статистическим лагранжианом

${\displaystyle {\mathcal {L}}=(f(t)-1)^{2}\,,}$

и уравнения движения для ж полученный от экстремизма действия S соответствующий L просто установите его равным 1. В физике такая величина «равна 1 как тождество оператора». В математике он «слабо сходится к 1». В любом случае он равен 1 для любого ожидаемого значения, или при усреднении по любому интервалу, или для всех практических целей.

Определение временного порядка для быть порядок оператора:

${\displaystyle [x,{\dot {x}}]=x{\frac {dx}{dt}}-{\frac {dx}{dt}}x=1}$

Это называется Лемма Ито в стохастическое исчисление, и (евклидовы) канонические коммутационные соотношения в физике.

Для общего статистического действия аналогичный аргумент показывает, что

${\displaystyle \left[x,{\frac {\partial S}{\partial {\dot {x}}}}\right]=1}$

и в квантовой механике дополнительная мнимая единица действия преобразует это в каноническое коммутационное соотношение,

${\displaystyle [x,p]=i}$

Частица в искривленном пространстве

Для частицы в искривленном пространстве кинетический член зависит от положения, и вышеупомянутое временное сечение не может быть применено, что является проявлением пресловутого проблема заказа оператора в квантовой механике Шредингера. Однако можно решить эту проблему, преобразовав временной интеграл по траекториям в плоском пространстве в искривленное пространство с помощью многозначного преобразования координат (неголономное отображение объяснил Вот ).

Факторы теории меры

Иногда (например, частица, движущаяся в искривленном пространстве) в функциональный интеграл также входят факторы теории меры:

${\displaystyle \int \mu [x]e^{iS[x]}\,{\mathcal {D}}x.}$

Этот фактор нужен для восстановления унитарности.

Например, если

${\displaystyle S=\int \left({\frac {m}{2}}g_{ij}{\dot {x}}^{i}{\dot {x}}^{j}-V(x)\right)\,dt,}$

то это означает, что каждый пространственный срез умножается на меру √грамм. Эту меру нельзя выразить как функционал, умножающий DИкс измерять, потому что они относятся к совершенно разным классам.

Ожидаемые значения и матричные элементы

Матричные элементы типа ${\displaystyle \langle x_{f}|e^{-{\frac {i}{\hbar }}{\hat {H}}(t-t')}F({\hat {x}})e^{-{\frac {i}{\hbar }}{\hat {H}}(t')}|x_{i}\rangle }$ принять форму

${\displaystyle \int _{x(0)=x_{i}}^{x(t)=x_{f}}{\mathcal {D}}[x]F(x(t'))e^{{\frac {i}{\hbar }}\int dtL(x(t),{\dot {x}}(t))}}$.

Это обобщается на несколько операторов, например

${\displaystyle \langle x_{f}|e^{-{\frac {i}{\hbar }}{\hat {H}}(t-t_{1})}F_{1}({\hat {x}})e^{-{\frac {i}{\hbar }}{\hat {H}}(t_{1}-t_{2})}F_{2}({\hat {x}})e^{-{\frac {i}{\hbar }}{\hat {H}}(t_{2})}|x_{i}\rangle =\int _{x(0)=x_{i}}^{x(t)=x_{f}}{\mathcal {D}}[x]F_{1}(x(t_{1}))F_{2}(x(t_{2}))e^{{\frac {i}{\hbar }}\int dtL(x(t),{\dot {x}}(t))}}$,

и к общему математическому ожиданию

${\displaystyle \langle F\rangle ={\frac {\int {\mathcal {D}}[\phi ]F(\phi )e^{{\frac {i}{\hbar }}S[\phi ]}}{\int {\mathcal {D}}[\phi ]e^{{\frac {i}{\hbar }}S[\phi ]}}}}$.

Евклидовы интегралы по путям

В интегралах по путям очень часто выполняется Вращение фитиля от реального до мнимого времени. В контексте квантовой теории поля вращение Вика изменяет геометрию пространства-времени с лоренцевой на евклидову; в результате интегралы по траекториям с поворотом Вика часто называют евклидовыми интегралами по траекториям.

Вращение Вика и формула Фейнмана – Каца.

Если мы заменим ${\displaystyle t}$ к ${\displaystyle -it}$, оператор эволюции во времени ${\displaystyle e^{-it{\hat {H}}/\hbar }}$ заменяется на ${\displaystyle e^{-t{\hat {H}}/\hbar }}$. (Это изменение известно как Вращение фитиля.) Если мы повторим вывод формулы интеграла по путям в этом случае, мы получим^[10]

${\displaystyle \psi (x,t)={\frac {1}{Z}}\int _{\mathbf {x} (0)=x}e^{-S_{\mathrm {Euclidean} }(\mathbf {x} ,{\dot {\mathbf {x} }})/\hbar }\psi _{0}(\mathbf {x} (t))\,{\mathcal {D}}\mathbf {x} \,}$,

куда ${\displaystyle S_{\mathrm {Euclidean} }}$ евклидово действие, заданное формулой

${\displaystyle S_{\mathrm {Euclidean} }(\mathbf {x} ,{\dot {\mathbf {x} }})=\int \left[{\frac {m}{2}}|{\dot {\mathbf {x} }}(t)|^{2}+V(\mathbf {x} (t))\right]\,dt}$.

Обратите внимание на изменение знака между этим и нормальным действием, когда член потенциальной энергии отрицательный. (Период, термин Евклидово взяты из контекста квантовой теории поля, где переход от реального к мнимому времени меняет геометрию пространства-времени с лоренцевой на евклидову.)

Теперь вклад кинетической энергии в интеграл по путям выглядит следующим образом:

${\displaystyle {\frac {1}{Z}}\int _{\mathbf {x} (0)=x}f(\mathbf {x} )e^{-{\frac {m}{2}}\int |{\dot {\mathbf {x} }}|^{2}dt}\,{\mathcal {D}}\mathbf {x} \,}$

куда ${\displaystyle f(\mathbf {x} )}$ включает всю оставшуюся зависимость подынтегрального выражения от пути. Этот интеграл имеет строгую математическую интерпретацию как интегрирование против Мера Винера, обозначенный ${\displaystyle \mu _{x}}$. Мера Винера, построенная Норберт Винер дает прочную основу для Математическая модель броуновского движения Эйнштейна. Нижний индекс ${\displaystyle x}$ указывает, что мера ${\displaystyle \mu _{x}}$ поддерживается на дорожках ${\displaystyle \mathbf {x} }$ с ${\displaystyle \mathbf {x} (0)=x}$.

Тогда у нас есть строгая версия интеграла по путям Фейнмана, известная как Формула Фейнмана – Каца:^[11]

${\displaystyle \psi (x,t)=\int e^{-\int V(\mathbf {x} (t)\,dt/\hbar }\,\psi _{0}(\mathbf {x} (t))\,d\mu _{x}(\mathbf {x} )}$,

где сейчас ${\displaystyle \psi (x,t)}$ удовлетворяет версии уравнения Шредингера с вращением Вика,

${\displaystyle \hbar {\frac {\partial }{\partial t}}\psi (x,t)=-{\hat {H}}\psi (x,t)}$.

Хотя уравнение Шредингера с вращением Вика не имеет прямого физического смысла, интересные свойства оператора Шредингера ${\displaystyle {\hat {H}}}$ можно извлечь, изучив его.^[12]

Большая часть исследований квантовых теорий поля с точки зрения интегралов по траекториям, как в математической, так и в физической литературе, проводится в евклидовой обстановке, то есть после вращения Вика. В частности, есть различные результаты, показывающие, что, если можно построить евклидову теорию поля с подходящими свойствами, можно отменить вращение Вика, чтобы восстановить физическую, лоренцеву теорию.^[13] С другой стороны, гораздо труднее придать смысл интегралам по траекториям (даже евклидовым интегралам по траекториям) в квантовой теории поля, чем в квантовой механике.^[14]

Интеграл по путям и статистическая сумма

Интеграл по путям - это просто обобщение указанного выше интеграла на все квантово-механические задачи:

${\displaystyle Z=\int e^{\frac {i{\mathcal {S}}[\mathbf {x} ]}{\hbar }}\,{\mathcal {D}}\mathbf {x} \quad {\text{where }}{\mathcal {S}}[\mathbf {x} ]=\int _{0}^{T}L[\mathbf {x} (t),{\dot {\mathbf {x} }}(t)]\,dt}$

это действие классической задачи, в которой исследуется путь, начинающийся в момент времени т = 0 и заканчивается во времени т = Т, и ${\displaystyle {\mathcal {D}}\mathbf {x} }$ обозначает интеграцию по всем путям. В классическом пределе ${\displaystyle {\mathcal {S}}[\mathbf {x} ]\gg \hbar }$, путь минимального действия доминирует над интегралом, потому что фаза любого пути от него быстро флуктуирует, и различные вклады сокращаются.^[15]

Связь с статистическая механика следует. Принимая во внимание только пути, которые начинаются и заканчиваются одной и той же конфигурацией, выполните Вращение фитиля Это = τ, то есть сделать время воображаемым и интегрировать по всем возможным конфигурациям начала-конца. Интеграл по траекториям с вращением Вика, описанный в предыдущем подразделе, в котором обычное действие заменено его «евклидовым» аналогом, теперь напоминает функция распределения статистической механики, определенной в канонический ансамбль с обратной температурой, пропорциональной мнимому времени, 1/Т = k_Bτ/час. Однако, строго говоря, это статистическая сумма для статистическая теория поля.

Ясно, что такая глубокая аналогия между квантовой механикой и статистической механикой не может зависеть от формулировки. В канонической формулировке видно, что унитарный оператор эволюции состояния задается выражением

${\displaystyle |\alpha ;t\rangle =e^{-{\frac {iHt}{\hbar }}}|\alpha ;0\rangle }$

где государство α развивается со временем т = 0. Если сделать здесь вращение фитиля и найти амплитуду перехода из любого состояния обратно в то же состояние за (мнимое) время Это дан кем-то

${\displaystyle Z=\operatorname {Tr} \left[e^{\frac {-HT}{\hbar }}\right]}$

что в точности является статистической суммой статистической механики для той же системы при температуре, указанной ранее. Один аспект этой эквивалентности был также известен Эрвин Шредингер который заметил, что уравнение, названное в его честь, выглядело как уравнение диффузии после вращения фитиля. Обратите внимание, однако, что евклидов интеграл по путям на самом деле имеет форму классический модель статистической механики.

Квантовая теория поля

Оба подхода Шредингера и Гейзенберга к квантовой механике выделяют время и не соответствуют духу теории относительности. Например, подход Гейзенберга требует, чтобы операторы скалярного поля подчинялись коммутационному соотношению

${\displaystyle [\varphi (x),\partial _{t}\varphi (y)]=i\delta ^{3}(x-y)}$

для двух одновременных пространственных положений Икс и у, и это не релятивистски инвариантное понятие. Результаты расчета находятся ковариантны, но на промежуточных стадиях симметрия не проявляется. Если бы наивные теоретико-полевые расчеты не давали бесконечных ответов в континуальном пределе, это не было бы такой большой проблемой - это был бы просто неправильный выбор координат. Но отсутствие симметрии означает, что бесконечные величины должны быть отрезаны, а плохие координаты делают практически невозможным отрезание теории без нарушения симметрии. Это затрудняет получение физических прогнозов, которые требуют тщательная процедура ограничения.

Проблема утраченной симметрии также возникает в классической механике, где гамильтонова формулировка также поверхностно выделяет время. Лагранжева формулировка делает очевидной релятивистскую инвариантность. Точно так же интеграл по путям явно релятивистский. Он воспроизводит уравнение Шредингера, уравнения движения Гейзенберга и канонические коммутационные соотношения и показывает, что они совместимы с теорией относительности. Он расширяет операторную алгебру типа Гейзенберга на правила продукта оператора, которые являются новыми отношениями, которые трудно увидеть в старом формализме.

Кроме того, разный выбор канонических переменных приводит к очень разным формулировкам одной и той же теории. Преобразования между переменными могут быть очень сложными, но интеграл по путям превращает их в достаточно простые изменения переменных интегрирования. По этим причинам интеграл по путям Фейнмана сделал более ранние формализмы в значительной степени устаревшими.

Цена представления интеграла по путям состоит в том, что унитарность теории больше не является самоочевидной, но ее можно доказать, заменив переменные на некоторое каноническое представление. Сам интеграл по путям также имеет дело с более крупными математическими пространствами, чем обычно, что требует более тщательной математики, не все из которых были полностью разработаны. Исторически сложилось так, что интеграл по путям не был принят сразу, отчасти потому, что для правильного включения фермионов потребовалось много лет. Это потребовало от физиков изобрести совершенно новый математический объект - Переменная Грассмана - что также позволило естественным образом изменять переменные, а также ограниченное квантование.

Переменные интегрирования в интеграле по путям слегка не коммутируют. Значение произведения двух операторов поля в том, что выглядит как одна и та же точка, зависит от того, как эти две точки упорядочены в пространстве и времени. Это делает некоторые наивные идентичности провал.

Пропагатор

В релятивистских теориях для каждой теории есть как частица, так и поле. Представление поля - это сумма по всем конфигурациям поля, а представление частицы - это сумма по различным траекториям частиц.

Нерелятивистская формулировка традиционно дается в терминах траекторий частиц, а не полей. Здесь интеграл по путям в обычных переменных с фиксированными граничными условиями дает амплитуду вероятности выхода частицы из точки Икс В точку у во время Т:

${\displaystyle K(x,y;T)=\langle y;T\mid x;0\rangle =\int _{x(0)=x}^{x(T)=y}e^{iS[x]}\,Dx.}$

Это называется пропагатор. Наложение разных значений начальной позиции Икс с произвольным начальным состоянием ψ₀(Икс) строит конечное состояние:

${\displaystyle \psi _{T}(y)=\int _{x}\psi _{0}(x)K(x,y;T)\,dx=\int ^{x(T)=y}\psi _{0}(x(0))e^{iS[x]}\,Dx.}$

Для пространственно однородной системы, где K(Икс, у) это только функция (Икс − у), интеграл есть свертка, конечное состояние - это начальное состояние, связанное с пропагатором:

${\displaystyle \psi _{T}=\psi _{0}*K(;T).}$

Для свободной частицы массы м, пропагатор может быть вычислен либо явно из интеграла по путям, либо с учетом того, что уравнение Шредингера является уравнением диффузии в мнимом времени, и решение должно быть нормализованным гауссовым:

${\displaystyle K(x,y;T)\propto e^{\frac {im(x-y)^{2}}{2T}}.}$

Взяв преобразование Фурье в (Икс − у) производит еще один гауссиан:

${\displaystyle K(p;T)=e^{\frac {iTp^{2}}{2m}},}$

И в п-пространственный коэффициент пропорциональности здесь постоянен во времени, что мы сейчас проверим. Преобразование Фурье во времени, расширяющее K(п; Т) равным нулю для отрицательных времен, дает функцию Грина или пропагатор в частотном пространстве:

${\displaystyle G_{\text{F}}(p,E)={\frac {-i}{E-{\frac {{\vec {p}}^{2}}{2m}}+i\varepsilon }},}$

который является обратным к оператору, который аннулирует волновую функцию в уравнении Шредингера, которое не получилось бы правильным, если бы коэффициент пропорциональности не был постоянным в п-пространственное представление.

Бесконечно малый член в знаменателе - это небольшое положительное число, которое гарантирует, что обратное преобразование Фурье в E будет отличным от нуля только в будущем. В прошлые времена контур обратного преобразования Фурье замыкается к значениям E где нет особенности. Это гарантирует, что K распространяет частицу в будущее и является причиной индекса "F" на грамм. Бесконечно малый член можно интерпретировать как бесконечно малое вращение к мнимому времени.

Также возможно заново выразить нерелятивистскую эволюцию во времени в терминах пропагаторов, идущих в прошлое, поскольку уравнение Шредингера обратимо во времени. Прошлый пропагатор такой же, как и будущий пропагатор, за исключением очевидной разницы, что он исчезает в будущем, а в гауссовском т заменяется на −т. В этом случае интерпретация состоит в том, что это величины, которые сворачивают окончательную волновую функцию, чтобы получить начальную волновую функцию:

${\displaystyle G_{\text{B}}(p,E)={\frac {-i}{-E-{\frac {i{\vec {p}}^{2}}{2m}}+i\varepsilon }}.}$

Учитывая почти идентичное единственное изменение, это признак E и ε, параметр E в функции Грина может быть либо энергия, если пути ведут в будущее, либо отрицательная энергия, если пути ведут в прошлое.

Для нерелятивистской теории время, измеренное на пути движущейся частицы, и время, измеренное сторонним наблюдателем, одинаковы. В теории относительности это уже неверно. Для релятивистской теории пропагатор должен быть определен как сумма всех путей, которые проходят между двумя точками за фиксированное собственное время, измеренное вдоль пути (эти пути описывают траекторию частицы в пространстве и во времени):

${\displaystyle K(x-y,\mathrm {T} )=\int _{x(0)=x}^{x(\mathrm {T} )=y}e^{i\int _{0}^{\mathrm {T} }{\sqrt {{\dot {x}}^{2}}}-\alpha \,d\tau }.}$

Приведенный выше интеграл нетривиально интерпретировать из-за квадратного корня. К счастью, есть эвристический трюк. Сумма соответствует релятивистской длине дуги пути колеблющейся величины, и, как и нерелятивистский интеграл по путям, следует интерпретировать как слегка повернутый в мнимое время. Функция K(Икс − у, τ) можно вычислить, когда сумма превышает пути в евклидовом пространстве:

${\displaystyle K(x-y,\mathrm {T} )=e^{-\alpha \mathrm {T} }\int _{x(0)=x}^{x(\mathrm {T} )=y}e^{-L}.}$

Это описывает сумму по всем путям длины Τ экспоненты минус длина. Этому можно дать вероятностную интерпретацию. Сумма по всем путям - это средняя вероятность по пути, построенному шаг за шагом. Общее количество шагов пропорционально Τ, и тем меньше вероятность каждого шага, чем он длиннее. Посредством Центральная предельная теорема, результатом многих независимых шагов является гауссиан с дисперсией, пропорциональной Τ:

${\displaystyle K(x-y,\mathrm {T} )=e^{-\alpha \mathrm {T} }e^{-{\frac {(x-y)^{2}}{\mathrm {T} }}}.}$

Обычное определение релятивистского пропагатора требует только амплитуды: он должен двигаться от Икс к у, после суммирования всех возможных подходящих времен, которые могут потребоваться:

${\displaystyle K(x-y)=\int _{0}^{\infty }K(x-y,\mathrm {T} )W(\mathrm {T} )\,d\mathrm {T} ,}$

куда W(Τ) - весовой коэффициент, относительная важность путей разного собственного времени. Благодаря трансляционной симметрии в собственное время, этот вес может быть только экспоненциальным множителем и может быть поглощен постоянным α:

${\displaystyle K(x-y)=\int _{0}^{\infty }e^{-{\frac {(x-y)^{2}}{\mathrm {T} }}-\alpha \mathrm {T} }\,d\mathrm {T} .}$

Это Представительство Швингера. Преобразование Фурье по переменной (Икс − у) можно сделать для каждого значения Τ отдельно, и потому что каждый отдельный Τ вклад является гауссовским, дает преобразование Фурье которого является другим гауссовским с обратной шириной. Так что в п-space, пропагатор может быть просто перевыражен:

${\displaystyle K(p)=\int _{0}^{\infty }e^{-\mathrm {T} p^{2}-\mathrm {T} \alpha }\,d\mathrm {T} ={\frac {1}{p^{2}+\alpha }},}$

который является евклидовым пропагатором для скалярной частицы. Вращающийся п₀ быть воображаемым дает обычный релятивистский пропагатор с точностью до множителя −я и двусмысленность, которая будет разъяснена ниже:

${\displaystyle K(p)={\frac {i}{p_{0}^{2}-{\vec {p}}^{2}-m^{2}}}.}$

Это выражение можно интерпретировать в нерелятивистском пределе, где его удобно разбить на частичные фракции:

${\displaystyle 2p_{0}K(p)={\frac {i}{p_{0}-{\sqrt {{\vec {p}}^{2}+m^{2}}}}}+{\frac {i}{p_{0}+{\sqrt {{\vec {p}}^{2}+m^{2}}}}}.}$

Для состояний, в которых присутствует одна нерелятивистская частица, начальная волновая функция имеет распределение частот, сосредоточенное около п₀ = м. При свертке с пропагатором, который в п пробел просто означает умножение на пропагатор, второй член подавляется, а первый член усиливается. Для частот около п₀ = м, доминирующий первый член имеет вид

${\displaystyle 2mK_{\text{NR}}(p)={\frac {i}{(p_{0}-m)-{\frac {{\vec {p}}^{2}}{2m}}}}.}$

Это выражение для нерелятивистской Функция Грина свободной частицы Шредингера.

Второй член также имеет нерелятивистский предел, но этот предел сосредоточен на отрицательных частотах. Во втором полюсе преобладают вклады от траекторий, где собственное время и координатное время идут в противоположном смысле, что означает, что второй член следует интерпретировать как античастица. Нерелятивистский анализ показывает, что в этой форме античастица все еще имеет положительную энергию.

Правильный способ выразить это математически: добавив в свое время небольшой коэффициент подавления, предел, в котором т → −∞ первого члена должна исчезнуть, а т → +∞ предел второго члена должен исчезнуть. В преобразовании Фурье это означает сдвиг полюса в п₀ немного, так что обратное преобразование Фурье подберет небольшой коэффициент затухания в одном из направлений времени:

${\displaystyle K(p)={\frac {i}{p_{0}-{\sqrt {{\vec {p}}^{2}+m^{2}}}+i\varepsilon }}+{\frac {i}{p_{0}-{\sqrt {{\vec {p}}^{2}+m^{2}}}-i\varepsilon }}.}$

Без этих членов нельзя было бы однозначно оценить полюсный вклад при выполнении обратного преобразования Фурье п₀. Термины можно перекомбинировать:

${\displaystyle K(p)={\frac {i}{p^{2}-m^{2}+i\varepsilon }},}$

который при факторизации дает бесконечно малые члены противоположного знака в каждом множителе. Это математически точная форма пропагатора релятивистских частиц, свободная от каких-либо двусмысленностей. В ε термин вводит небольшую мнимую часть в α = м², который в версии Минковского представляет собой небольшое экспоненциальное подавление длинных путей.

Таким образом, в релятивистском случае представление пропагатора в виде интеграла по путям Фейнмана включает в себя пути, идущие назад во времени, которые описывают античастицы. Пути, которые вносят вклад в релятивистский пропагатор, идут вперед и назад во времени, а интерпретация Это связано с тем, что амплитуда движения свободной частицы между двумя точками включает в себя амплитуды, когда частица флуктуирует в античастицу, перемещается назад во времени, а затем снова вперед.

В отличие от нерелятивистского случая, релятивистскую теорию локального распространения частиц невозможно построить без включения античастиц. Все локальные дифференциальные операторы имеют инверсии, отличные от нуля вне светового конуса, а это означает, что невозможно удержать частицу от движения со скоростью, превышающей скорость света. Такая частица не может иметь функцию Грина, которая будет отличаться от нуля только в будущем в релятивистски инвариантной теории.

Функционалы полей

Однако формулировка интеграла по путям также чрезвычайно важна в непосредственный применение к квантовой теории поля, в которой рассматриваемые «пути» или истории - это не движения отдельной частицы, а возможные временные эволюции поле по всему пространству. Это действие технически называется функциональный поля: S[ϕ], где поле ϕ(Икс^μ) сам по себе является функцией пространства и времени, а квадратные скобки напоминают, что действие зависит от всех значений поля везде, а не только от какого-то конкретного значения. Один такая заданная функция ϕ(Икс^μ) из пространство-время называется конфигурация поля. В принципе, интегрируют амплитуду Фейнмана по классу всех возможных конфигураций поля.

Большая часть формального исследования КТП посвящена свойствам получаемого функционального интеграла, и было приложено много усилий (пока не совсем успешных) для их получения. функциональные интегралы математически точный.

Такой функциональный интеграл очень похож на функция распределения в статистическая механика. Действительно, иногда бывает называется а функция распределения, и эти два по существу математически идентичны, за исключением фактора я в показателе степени в постулате Фейнмана 3. Аналитическое продолжение интеграл от мнимой переменной времени (называемой Вращение фитиля ) делает функциональный интеграл даже более похожим на статистическую статистическую сумму, а также устраняет некоторые математические трудности работы с этими интегралами.

Ожидаемые ценности

В квантовая теория поля, если действие дается функциональный S конфигураций полей (которые зависят только локально от полей), то по расписанию ожидаемое значение вакуума из полиномиально ограниченный функциональный F, ⟨F⟩, дан кем-то

${\displaystyle \langle F\rangle ={\frac {\int {\mathcal {D}}\varphi F[\varphi ]e^{i{\mathcal {S}}[\varphi ]}}{\int {\mathcal {D}}\varphi e^{i{\mathcal {S}}[\varphi ]}}}.}$

Символ ∫Dϕ вот краткий способ представить бесконечномерный интеграл по всем возможным конфигурациям поля во всем пространстве-времени. Как указано выше, простой интеграл по путям в знаменателе обеспечивает правильную нормализацию.

Как вероятность

Строго говоря, единственный вопрос, который можно задать в физике: Какая доля состояний удовлетворяет условию А также удовлетворяют условию B? Ответом на это будет число от 0 до 1, которое можно интерпретировать как условная возможность, записанный как П(B|А). С точки зрения интеграции пути, поскольку П(B|А) = П(А∩B) / П(А), это означает

${\displaystyle \operatorname {P} (B\mid A)={\frac {\sum _{F\subset A\cap B}\left|\int {\mathcal {D}}\varphi O_{\text{in}}[\varphi ]e^{i{\mathcal {S}}[\varphi ]}F[\varphi ]\right|^{2}}{\sum _{F\subset A}\left|\int {\mathcal {D}}\varphi O_{\text{in}}[\varphi ]e^{i{\mathcal {S}}[\varphi ]}F[\varphi ]\right|^{2}}},}$

где функционал О_в[ϕ] представляет собой суперпозицию всех входящих состояний, которые могут привести к состояниям, которые нас интересуют. В частности, это может быть состояние, соответствующее состоянию Вселенной сразу после Большой взрыв, хотя для реальных расчетов это можно упростить с помощью эвристических методов. Поскольку это выражение является частным интегралов по путям, оно естественно нормализуется.

Уравнения Швингера – Дайсона

Основная статья: Уравнение Швингера – Дайсона

Поскольку эта формулировка квантовой механики аналогична классическому принципу действия, можно ожидать, что тождества, касающиеся действия в классической механике, будут иметь квантовые аналоги, выводимые из функционального интеграла. Так бывает часто.

На языке функционального анализа мы можем написать Уравнения Эйлера – Лагранжа. в качестве

${\displaystyle {\frac {\delta {\mathcal {S}}[\varphi ]}{\delta \varphi }}=0}$

(левая часть - функциональная производная; уравнение означает, что действие стационарно при небольших изменениях конфигурации поля). Квантовые аналоги этих уравнений называются Уравнения Швингера – Дайсона.

Если функциональная мера Dϕ оказывается трансляционно инвариантный (мы предполагаем это до конца этой статьи, хотя это не так, скажем, нелинейные сигма-модели ), а если предположить, что после Вращение фитиля

${\displaystyle e^{i{\mathcal {S}}[\varphi ]},}$

который теперь становится

${\displaystyle e^{-H[\varphi ]}}$

для некоторых ЧАС, он стремится к нулю быстрее, чем взаимный любой многочлен для больших значений φ, тогда мы можем интегрировать по частям (после вращения Вика, за которым следует обратное вращение Вика), чтобы получить следующие уравнения Швингера-Дайсона для математического ожидания:

${\displaystyle \left\langle {\frac {\delta F[\varphi ]}{\delta \varphi }}\right\rangle =-i\left\langle F[\varphi ]{\frac {\delta {\mathcal {S}}[\varphi ]}{\delta \varphi }}\right\rangle }$

для любого полиномиально ограниченного функционала F. в обозначение де Витта это похоже^[16]

${\displaystyle \left\langle F_{,i}\right\rangle =-i\left\langle F{\mathcal {S}}_{,i}\right\rangle .}$

Эти уравнения являются аналогом на оболочке Уравнения EL. Упорядочение по времени берется до производных по времени внутри S_,я.

Если J (называется исходное поле ) является элементом двойное пространство конфигураций поля (которое имеет не менее аффинная структура из-за предположения трансляционная инвариантность для функциональной меры), то производящий функционал Z исходных полей определенный быть

${\displaystyle Z[J]=\int {\mathcal {D}}\varphi e^{i\left({\mathcal {S}}[\varphi ]+\langle J,\varphi \rangle \right)}.}$

Обратите внимание, что

${\displaystyle {\frac {\delta ^{n}Z}{\delta J(x_{1})\cdots \delta J(x_{n})}}[J]=i^{n}\,Z[J]\,\left\langle \varphi (x_{1})\cdots \varphi (x_{n})\right\rangle _{J},}$

или же

${\displaystyle Z^{,i_{1}\cdots i_{n}}[J]=i^{n}Z[J]\left\langle \varphi ^{i_{1}}\cdots \varphi ^{i_{n}}\right\rangle _{J},}$

куда

${\displaystyle \langle F\rangle _{J}={\frac {\int {\mathcal {D}}\varphi F[\varphi ]e^{i\left({\mathcal {S}}[\varphi ]+\langle J,\varphi \rangle \right)}}{\int {\mathcal {D}}\varphi e^{i\left({\mathcal {S}}[\varphi ]+\langle J,\varphi \rangle \right)}}}.}$

В принципе, если Dφ е^яS[φ] рассматривается как функциональное распределение (не следует воспринимать это слишком буквально как интерпретацию QFT в отличие от вращающегося фитилем статистическая механика аналог, потому что у нас заказ времени тут осложнения!), то ⟨φ(Икс₁) ... φ(Икс_п)⟩ это его моменты, и Z это его преобразование Фурье.

Если F является функционалом φ, то для оператор K, F[K] определяется как оператор, который заменяет K за φ. Например, если

${\displaystyle F[\varphi ]={\frac {\partial ^{k_{1}}}{\partial x_{1}^{k_{1}}}}\varphi (x_{1})\cdots {\frac {\partial ^{k_{n}}}{\partial x_{n}^{k_{n}}}}\varphi (x_{n}),}$

и грамм является функционалом J, тогда

${\displaystyle F\left[-i{\frac {\delta }{\delta J}}\right]G[J]=(-i)^{n}{\frac {\partial ^{k_{1}}}{\partial x_{1}^{k_{1}}}}{\frac {\delta }{\delta J(x_{1})}}\cdots {\frac {\partial ^{k_{n}}}{\partial x_{n}^{k_{n}}}}{\frac {\delta }{\delta J(x_{n})}}G[J].}$

Тогда из свойств функциональные интегралы

${\displaystyle \left\langle {\frac {\delta {\mathcal {S}}}{\delta \varphi (x)}}[\varphi ]+J(x)\right\rangle _{J}=0}$

мы получаем «основное» уравнение Швингера – Дайсона:

${\displaystyle {\frac {\delta {\mathcal {S}}}{\delta \varphi (x)}}\left[-i{\frac {\delta }{\delta J}}\right]Z[J]+J(x)Z[J]=0,}$

или же

${\displaystyle {\mathcal {S}}_{,i}[-i\partial ]Z+J_{i}Z=0.}$

Если функциональная мера не является трансляционно-инвариантной, ее можно было бы выразить как продукт M[φ] Dφ, куда M это функциональный и Dφ - трансляционно-инвариантная мера. Это верно, например, для нелинейных сигма-моделей, где целевое пространство диффеоморфен р^п. Однако если целевой коллектор - какое-то топологически нетривиальное пространство, понятие трансляции даже не имеет смысла.

В этом случае нам придется заменить S в этом уравнении другим функционалом

${\displaystyle {\hat {\mathcal {S}}}={\mathcal {S}}-i\ln M.}$

Если мы расширим это уравнение как Серия Тейлор о J = 0, получаем всю систему уравнений Швингера – Дайсона.

Локализация

Интегралы по путям обычно считаются суммой всех путей в бесконечном пространстве-времени. Однако в локальная квантовая теория поля мы бы ограничили все, чтобы лежать в пределах конечного причинно полный область, например, внутри двойного светового конуса. Это дает более математически точное и физически строгое определение квантовой теории поля.

Личности Уорда-Такахаши

Основная статья: Идентичность Уорда – Такахаши

А как насчет на оболочке Теорема Нётер для классического корпуса? Есть ли у него квантовый аналог? Да, но с одной оговоркой. Функциональная мера также должна быть инвариантной относительно однопараметрической группы преобразования симметрии.

Давайте просто предположим здесь для простоты, что рассматриваемая симметрия является локальной (не локальной в смысле калибровочная симметрия, но в том смысле, что преобразованное значение поля в любой заданной точке при бесконечно малом преобразовании будет зависеть только от конфигурации поля в произвольно малой окрестности рассматриваемой точки). Предположим также, что действие является локальным в том смысле, что оно является интегралом по пространству-времени Лагранжиан, и это

${\displaystyle Q[{\mathcal {L}}(x)]=\partial _{\mu }f^{\mu }(x)}$

для какой-то функции ж куда ж зависит только локально от φ (и, возможно, положение в пространстве-времени).

Если мы не предполагаем каких-либо особых граничных условий, это не будет «истинной» симметрией в истинном смысле этого слова в целом, если только ж = 0 или что-то. Здесь, Q это происхождение который генерирует рассматриваемую группу с одним параметром. Мы могли бы иметь антидеривации а также такие как BRST и суперсимметрия.

Предположим также

${\displaystyle \int {\mathcal {D}}\varphi \,Q[F][\varphi ]=0}$

для любого полиномиально ограниченного функционала F. Это свойство называется инвариантностью меры. И это в целом не выполняется. Видеть аномалия (физика) Больше подробностей.

Потом,

${\displaystyle \int {\mathcal {D}}\varphi \,Q\left[Fe^{iS}\right][\varphi ]=0,}$

что подразумевает

${\displaystyle \langle Q[F]\rangle +i\left\langle F\int _{\partial V}f^{\mu }\,ds_{\mu }\right\rangle =0}$

где интеграл идет по границе. Это квантовый аналог теоремы Нётер.

Теперь предположим еще дальше, что Q является локальным интегралом

${\displaystyle Q=\int d^{d}x\,q(x)}$

куда

${\displaystyle q(x)[\varphi (y)]=\delta ^{(d)}(X-y)Q[\varphi (y)]\,}$

так что

${\displaystyle q(x)[S]=\partial _{\mu }j^{\mu }(x)\,}$

куда

${\displaystyle j^{\mu }(x)=f^{\mu }(x)-{\frac {\partial }{\partial (\partial _{\mu }\varphi )}}{\mathcal {L}}(x)Q[\varphi ]\,}$

(предполагается, что лагранжиан зависит только от φ и его первые частные производные! Более общие лагранжианы потребуют модификации этого определения!). Мы не настаиваем на этом q(Икс) является генератором симметрии (т.е. мы нет настаивая на принцип измерения ), но только это Q является. И мы также предполагаем еще более сильное предположение, что функциональная мера локально инвариантна:

${\displaystyle \int {\mathcal {D}}\varphi \,q(x)[F][\varphi ]=0.}$

Тогда у нас было бы

${\displaystyle \langle q(x)[F]\rangle +i\langle Fq(x)[S]\rangle =\langle q(x)[F]\rangle +i\left\langle F\partial _{\mu }j^{\mu }(x)\right\rangle =0.}$

В качестве альтернативы,

${\displaystyle q(x)[S]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]+J(x)Q[\varphi (x)]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]=\partial _{\mu }j^{\mu }(x)\left[-i{\frac {\delta }{\delta J}}\right]Z[J]+J(x)Q[\varphi (x)]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]=0.}$

Приведенные выше два уравнения являются Личности Уорда-Такахаши.

Теперь для случая, когда ж = 0, мы можем забыть обо всех граничных условиях и предположениях о локальности. У нас просто было бы

${\displaystyle \left\langle Q[F]\right\rangle =0.}$

В качестве альтернативы,

${\displaystyle \int d^{d}x\,J(x)Q[\varphi (x)]\left[-i{\frac {\delta }{\delta J}}\right]Z[J]=0.}$

Предостережения

Потребность в регуляторах и перенормировке

Интегралы по путям, как они здесь определены, требуют введения регуляторы. Изменение шкалы регулятора приводит к ренормгруппа. Фактически, перенормировка является основным препятствием на пути к правильному определению интегралов по путям.

Заказ рецепта

Независимо от того, работает ли человек в конфигурационном или фазовом пространстве, при равенстве операторный формализм и формулировка интеграла по путям, предписание упорядочения требуется для разрешения неоднозначности в соответствии между некоммутативными операторами и коммутативными функциями, которые появляются в подынтегральных выражениях по путям. Например, оператор ${\displaystyle {\frac {1}{2}}({\hat {q}}{\hat {p}}+{\hat {p}}{\hat {q}})}$ можно перевести как ${\displaystyle qp-{\frac {i\hbar }{2}}}$, ${\displaystyle qp+{\frac {i\hbar }{2}}}$, или же ${\displaystyle qp}$ в зависимости от того, выбираете ли вы ${\displaystyle {\hat {q}}{\hat {p}}}$, ${\displaystyle {\hat {p}}{\hat {q}}}$, или рецепт заказа Weyl; наоборот, ${\displaystyle qp}$ можно перевести на любой ${\displaystyle {\hat {q}}{\hat {p}}}$, ${\displaystyle {\hat {p}}{\hat {q}}}$, или же ${\displaystyle {\frac {1}{2}}({\hat {q}}{\hat {p}}+{\hat {p}}{\hat {q}})}$ для того же соответствующего выбора рецепта заказа.

Интеграл по путям в квантово-механической интерпретации

В одной интерпретация квантовой механики В интерпретации «сумма по историям» интеграл по путям считается фундаментальным, а реальность рассматривается как единый неразличимый «класс» путей, которые все имеют одни и те же события. Для такой интерпретации очень важно понимать, что именно представляет собой событие. Метод суммирования историй дает идентичные результаты канонической квантовой механике, а Синха и Соркин^[17] утверждают, что интерпретация объясняет Парадокс Эйнштейна – Подольского – Розена не прибегая к нелокальность.

Немного^{[ВОЗ? ]} сторонники интерпретации квантовой механики, подчеркивая декогеренция попытались сделать более строгую идею извлечения классической «крупнозернистой» истории из пространства всех возможных историй.

Квантовая гравитация

В то время как в квантовой механике формулировка интеграла по путям полностью эквивалентна другим формулировкам, вполне возможно, что ее можно распространить на квантовую гравитацию, что сделает ее отличной от Гильбертово пространство модель. Фейнман добился определенных успехов в этом направлении, и его работа была расширена на Хокинг и другие.^[18] Подходы, в которых используется этот метод, включают причинные динамические триангуляции и пенопласт модели.

Квантовое туннелирование

Квантовое туннелирование можно смоделировать, используя формирование интеграла по траекториям для определения действия траектории через потенциальный барьер. С использованием Приближение ВКБ, скорость туннелирования (Γ) можно определить как имеющую вид

${\displaystyle \Gamma =A_{\mathrm {o} }\exp \left(-{\frac {S_{\mathrm {eff} }}{\hbar }}\right)}$

с эффективным действием S_эфф и предэкспоненциальный множитель А_о. Эта форма особенно полезна в диссипативная система, в котором системы и окружение должны моделироваться вместе. С использованием Уравнение Ланжевена моделировать Броуновское движение, формирование интеграла по путям можно использовать для определения эффективного действия и предэкспоненциальной модели, чтобы увидеть влияние диссипации на туннелирование.^[19] С помощью этой модели можно предсказать скорость туннелирования макроскопических систем (при конечных температурах).

Смотрите также

• Теоретическое и экспериментальное обоснование уравнения Шредингера
• Статические силы и обмен виртуальными частицами
• Шахматная доска Фейнмана
• Березин интеграл
• Пропагаторы
• Теория поглотителя Уиллера – Фейнмана
• Формула Фейнмана – Каца

Замечания

1. Оба отметили, что в пределе действия, который велик по сравнению с уменьшенным Постоянная Планка час (с помощью натуральные единицы, час = 1) или классический предел, в интеграле по путям преобладают решения, которые находятся в окрестности стационарные точки действия.
2. Для упрощенного, пошагового вывода вышеуказанного соотношения см. Интегралы по путям в квантовых теориях: первый шаг педагогики.

Примечания

1. Вайнберг 2002, Глава 9.
2. Винокур 2015 Ошибка harvnb: нет цели: CITEREFVinokur2015 (помощь)
   PDF:Динамический вихревой переход Мотта
3. Чайчян, Демичев 2001
4. Дирак 1933
   PDF:Лагранжиан в квантовой механике
5. Ван Влек 1928
6. Дирак 1933
7. Хильке, М. «Введение в интегралы по путям» (PDF).
8. Дуру и Кляйнерт 1979, Глава 13.
9. Фейнман 1948
10. Зал 2013, Раздел 20.3.
11. Зал 2013, Теорема 20.3.
12. Саймон 1979
13. Glimm & Jaffe 1981, Глава 19. ошибка harvnb: несколько целей (2 ×): CITEREFGlimmJaffe1981 (помощь)
14. Краткое описание истоков этих трудностей см. Холл (2013 г., Раздел 20.6.)
15. Фейнман, Хиббс и Стайер, 2010 г., стр. 29–31
16. Жан Зинн-Джастин (2009), Scholarpedia 4(2):8674 .
17. Синха и Соркин 1991
18. Гелл-Манн 1993
19. Кальдейра и Леггетт, 1983

Рекомендации

• Ахмад, Ишфак (1971). Математические интегралы в квантовой природе. Ядро. С. 189–209.
• Albeverio, S .; Hoegh-Krohn., R. & Mazzucchi, S (2008). Математическая теория интеграла по траекториям Фейнмана. Конспект лекций по математике 523. Springer-Verlag. ISBN  9783540769569.
• Кальдейра, А.О.; Леггетт, А.Дж. (1983). «Квантовое туннелирование в диссипативной системе». Анналы физики. 149 (2): 374–456. Bibcode:1983AnPhy.149..374C. Дои:10.1016/0003-4916(83)90202-6.
• Картье, П.; ДеВитт-Моретт, Сесиль (1995). «Новый взгляд на функциональную интеграцию». Журнал математической физики. 36 (5): 2137–2340. arXiv:funct-an / 9602005. Bibcode:1995JMP .... 36.2237C. Дои:10.1063/1.531039. S2CID  119581543.
• Чайчян, М .; Демичев, А. П. (2001). "Вступление". Интегралы по путям в физике Том 1: Стохастический процесс и квантовая механика. Тейлор и Фрэнсис. п. 1ff. ISBN  978-0-7503-0801-4.
• ДеВитт-Моретт, К. (1972). «Интеграл по путям Фейнмана: определение без ограничения процедуры». Коммуникации по математической физике. 28 (1): 47–67. Bibcode:1972CMaPh..28 ... 47D. Дои:10.1007 / BF02099371. МИСТЕР  0309456. S2CID  119669964.
• Дирак, Поль А. М. (1933). «Лагранжиан в квантовой механике» (PDF). Physikalische Zeitschrift der Sowjetunion. 3: 64–72.
• Дуру, И. ЧАС.; Кляйнерт, Хаген (1979). «Решение интеграла по путям для H-атома» (PDF). Письма по физике. 84B (2): 185–188. Bibcode:1979ФЛБ ... 84..185Д. Дои:10.1016/0370-2693(79)90280-6. Получено 2007-11-25.
• Этингоф, П (2002). «Геометрия и квантовая теория поля». MIT OpenCourseWare. Этот курс, разработанный для математиков, представляет собой строгое введение в пертурбативную квантовую теорию поля с использованием языка функциональных интегралов.
• Фейнман, Р. П. (2005) [1942/1948]. Браун, Л. М. (ред.). Тезис Фейнмана - новый подход к квантовой теории. World Scientific. Bibcode:2005ftna.book ..... B. Дои:10.1142/5852. ISBN  978-981-256-366-8. Диссертация 1942 г. Также включает статью Дирака 1933 года и публикацию Фейнмана 1948 года.
• Фейнман, Р. П. (1948). "Пространственно-временной подход к нерелятивистской квантовой механике" (PDF). Обзоры современной физики. 20 (2): 367–387. Bibcode:1948РвМП ... 20..367Ф. Дои:10.1103 / RevModPhys.20.367.
• Feynman, R.P .; Хиббс, А. Р. (1965). Квантовая механика и интегралы по траекториям. Нью-Йорк: Макгроу-Хилл. ISBN  978-0-07-020650-2. Историческая справка, написанная самим изобретателем формулировки интегрального пути и одним из его учеников.
• Feynman, R.P .; Хиббс, А.; Стайер, Д.Ф. (2010). Квантовая механика и интегралы по траекториям. Минеола, Нью-Йорк: Dover Publications. С. 29–31. ISBN  978-0-486-47722-0.
• Гелл-Манн, Мюррей (1993). «Большинство хороших вещей». In Brown, Laurie M .; Ригден, Джон С. (ред.). Воспоминания Ричарда Фейнмана. Американский институт физики. ISBN  978-0883188705.
• Глимм, Дж. И Джаффе, А (1981). Квантовая физика: функционально-интегральная точка зрения. Нью-Йорк: Springer-Verlag. ISBN  978-0-387-90562-4.
• Глимм, Дж. И Джаффе, А. (1981). Квантовая физика: функционально-интегральная точка зрения. Нью-Йорк: Springer-Verlag. ISBN  978-0-387-90562-4.
• Гроше, Кристиан и Штайнер, Франк (1998). Справочник по траекториям Фейнмана. Тракты Спрингера в современной физике 145. Springer-Verlag. ISBN  978-3-540-57135-3.
• Гроше, Кристиан (1992). "Введение в интеграл по путям Фейнмана". arXiv:hep-th / 9302097.
• Холл, Брайан К. (2013). Квантовая теория для математиков. Тексты для выпускников по математике. 267. Springer. Дои:10.1007/978-1-4614-7116-5. ISBN  978-1-4614-7115-8.
• Иномата, Акира; Курацудзи, Хироши; Джерри, Кристофер (1992). Интегралы по траекториям и когерентные состояния SU (2) и SU (1,1). Сингапур: World Scientific. ISBN  978-981-02-0656-7.
• Janke, W .; Пельстер, Аксель, ред. (2008). Интегралы по траекториям - новые тенденции и перспективы. Материалы 9-й Международной конференции. Мировое научное издательство. ISBN  978-981-283-726-4.
• Джонсон, Джеральд У .; Лапидус, Мишель Л. (2002). Интеграл Фейнмана и операционное исчисление Фейнмана. Оксфордские математические монографии. Издательство Оксфордского университета. ISBN  978-0-19-851572-2.
• Клаудер, Джон Р. (2010). Современный подход к функциональной интеграции. Нью-Йорк: Биркхойзер. ISBN  978-0-8176-4790-2.
• Кляйнерт, Хаген (2004). Интегралы по траекториям в квантовой механике, статистике, физике полимеров и финансовых рынках (4-е изд.). Сингапур: World Scientific. ISBN  978-981-238-107-1.
• Маккензи, Ричард (2000). «Методы интегрального пути и приложения». arXiv:Quant-ph / 0004090.
• Маццукки, С. (2009). Математические интегралы Фейнмана по путям и их приложения. World Scientific. ISBN  978-981-283-690-8.
• Мюллер-Кирстен, Харальд Дж. У. (2012). Введение в квантовую механику: уравнение Шредингера и интеграл по траекториям (2-е изд.). Сингапур: World Scientific.
• Риверс, Р. Дж. (1987). Методы интегралов по путям в квантовой теории поля. Издательство Кембриджского университета. ISBN  978-0-521-25979-8.
• Райдер, Льюис Х. (1985). Квантовая теория поля. Издательство Кембриджского университета. ISBN  978-0-521-33859-2. Хорошо читаемый учебник; введение в релятивистскую КТП для физики элементарных частиц.
• Шульман, Л. С. (1981). Методы и приложения интеграции путей. Нью-Йорк: Джон Вили и сыновья. ISBN  978-0-486-44528-1.
• Саймон, Б. (1979). Функциональная интеграция и квантовая физика. Нью-Йорк: Academic Press. ISBN  978-0-8218-6941-3.
• Синха, Суканья; Соркин, Рафаэль Д. (1991). "Суммарный отчет об эксперименте EPR (B)" (PDF). Основы письма по физике. 4 (4): 303–335. Bibcode:1991ФоФЛ ... 4..303С. Дои:10.1007 / BF00665892. S2CID  121370426.
• Томе, В.А. (1998). Интегралы по путям на групповых многообразиях.. Сингапур: World Scientific. ISBN  978-981-02-3355-6. Обсуждается определение интегралов по путям для систем, кинематические переменные которых являются генераторами вещественной сепарабельной связной группы Ли с неприводимыми квадратично интегрируемыми представлениями.
• Ван Влек, Дж. Х. (1928). «Принцип соответствия в статистической интерпретации квантовой механики». Труды Национальной академии наук Соединенных Штатов Америки. 14 (2): 178–188. Bibcode:1928ПНАС ... 14..178В. Дои:10.1073 / pnas.14.2.178. ЧВК  1085402. PMID  16577107.
• Вайнберг, С. (2002) [1995], Фонды, Квантовая теория полей, 1, Кембридж: Издательство Кембриджского университета, ISBN  978-0-521-55001-7
• Зи, А. (2010-02-21). Квантовая теория поля в двух словах (Второе изд.). Издательство Принстонского университета. ISBN  978-0-691-14034-6. Отличное введение в интегралы по путям (глава 1) и QFT в целом.
• Зинн Джастин, Дж. (2004). Интегралы по путям в квантовой механике. Издательство Оксфордского университета. ISBN  978-0-19-856674-8.

внешняя ссылка

• Интеграл по путям в Scholarpedia
• Интегралы по путям в квантовых теориях: первый шаг педагогики
• Математически строгий подход к пертурбативным интегралам по траекториям через анимацию на YouTube
• Бесконечные квантовые пути Фейнмана | PBS Space Time. 7 июля 2017 г. (Видео, 15:48)